Question

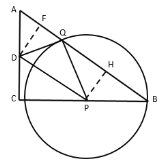
【题目】如图，在△ABC中，∠C=90°，AC=6，BC=8，P是线段BC上任意一点，以点P为圆心PB为半径的圆与线段AB相交于点Q（点Q与点A、B不重合），∠CPQ的角平分线与AC相交于点D．

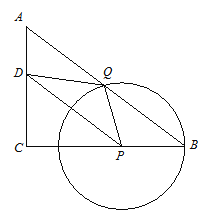
（1）如果DQ=PB，求证：四边形BQDP是平行四边形；

（2）设PB=x，△DPQ的面积为y，求y关于x的函数关系式，并写出x的取值范围；

（3）如果△ADQ是以DQ为腰的等腰三角形，求PB的长．

Answer 1

【答案】（1） 见解析；（2）； （3）4或或

【解析】

（1）根据角平分线的性质得到∠CPD=∠QPD，由DQ=PB=PQ得到∠QDP=∠QPD推出DQ∥BP，再根据DQ=BP推出四边形BQDP是平行四边形；

（2）先根据勾股定理求出AB=10，过点P作PH⊥AB于H，证明△BHP∽△BCA，求出BH=，HP=，根据同位角相等证明PD∥AB得到CD=，过点Q作QE⊥AC于E，利用三角函数求出QE=，再根据即可求出函数解析式，根据图形中各边都大于0得到不等式组求出x的取值范围；

（3）设PB=a，过点P作PH⊥AB，由（2）可知BQ=，则AQ=10-，分三种情况：①当AD=DQ时，②当AQ=DQ时，③当AD=AQ=10-时，分别求出a即可.

（1）∵∠CPQ的角平分线与AC相交于点D，

∴∠CPD=∠QPD，

∵DQ=PB=PQ，

∴∠QDP=∠QPD，

∴∠QDP=∠CPD，

∴DQ∥BP，

∵DQ=BP，

∴四边形BQDP是平行四边形；

（2）∵∠C=90°，AC=6，BC=8，

∴AB=10，

过点P作PH⊥AB于H，

∴∠BHP=∠C=90°，

∵∠B=∠B，

∴△BHP∽△BCA，

∴，

∴，

∴BH=，HP=，

∴BQ=2BH=，

∵PB=PQ，

∴∠B=∠BQP，

∵∠CPQ=2∠CPD=∠B+∠BQP，

∴∠CPQ=∠B，

∴PD∥AB，

∴，

∴，

∴CD=，

∴，

过点Q作QE⊥AC于E，

∵AQ=10-，

∴QE=，

∴

=

=

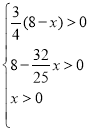∵，解得，

∴；

（3）设PB=a，

过点P作PH⊥AB，由（2）可知BQ=，∴AQ=10-，

①当AD=DQ时，如图，过点D作DF⊥AB于F，则AF=，

∴，

∴CD=，

∵PD∥AB，

∴,

∴，

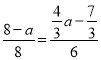解得a=4，

②当AQ=DQ时，过点Q作QM⊥AC于M，

∴AM===，

∴AD=2AM=，

∴CD=6-AD=,

∵PD∥AB，

∴,

∴,

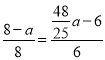解得a=；

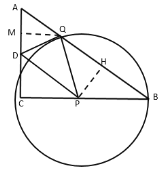
③当AD=AQ=10-时，则CD=6-AD=-4，

∵PD∥AB，

∴,

∴，

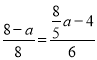解得a=.