题目内容
如图,抛物线的顶点坐标是(
,-
),且经过点A(8,14).
(1)求该抛物线的解析式;
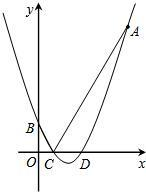
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连接AC、BC.试判断:PA+PB与AC+BC的大小关系,并说明理由.
| 5 |
| 2 |
| 9 |
| 8 |
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连接AC、BC.试判断:PA+PB与AC+BC的大小关系,并说明理由.

(1)设抛物线的解析式为y=a(x-
)2-
∵抛物线经过A(8,14),
∴14=a(8-
)2-
,
解得:a=
∴y=
(x-
)2-
(或y=
x2-
x+2)
(2)令x=0得y=2,
∴B(0,2)
令y=0得
x2-
x+2=0,
解得x1=1、x2=4
∴C(1,0)、D(4,0)
(3)结论:PA+PB≥AC+BC
理由是:①当点P与点C重合时,有PA+PB=AC+BC
②当点P异于点C时,
∵直线AC经过点A(8,14)、C(1,0),
∴直线AC的解析式为y=2x-2
设直线AC与y轴相交于点E,令x=0,得y=-2,
∴E(0,-2),
则点E(0,-2)与B(0,2)关于x轴对称
∴BC=EC,连接PE,则PE=PB,
∴AC+BC=AC+EC=AE,
∵在△APE中,有PA+PE>AE
∴PA+PB=PA+PE>AE=AC+BC
综上所得AP+BP≥AC+BC.

| 5 |
| 2 |
| 9 |
| 8 |
∵抛物线经过A(8,14),
∴14=a(8-
| 5 |
| 2 |
| 9 |
| 8 |
解得:a=
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
| 5 |
| 2 |
| 9 |
| 8 |
| 1 |
| 2 |
| 5 |
| 2 |
(2)令x=0得y=2,
∴B(0,2)
令y=0得
| 1 |
| 2 |
| 5 |
| 2 |
解得x1=1、x2=4
∴C(1,0)、D(4,0)
(3)结论:PA+PB≥AC+BC
理由是:①当点P与点C重合时,有PA+PB=AC+BC
②当点P异于点C时,
∵直线AC经过点A(8,14)、C(1,0),
∴直线AC的解析式为y=2x-2
设直线AC与y轴相交于点E,令x=0,得y=-2,
∴E(0,-2),
则点E(0,-2)与B(0,2)关于x轴对称
∴BC=EC,连接PE,则PE=PB,
∴AC+BC=AC+EC=AE,
∵在△APE中,有PA+PE>AE
∴PA+PB=PA+PE>AE=AC+BC
综上所得AP+BP≥AC+BC.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
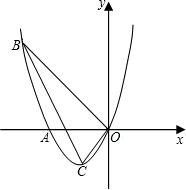
 点C的横坐标为1,
点C的横坐标为1,

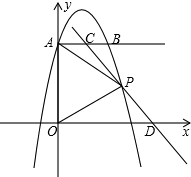 P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n. 在,请说明理由;
在,请说明理由;