题目内容
如图,正方形ABCD的边长为1,当点E在边BC上运动时(不与正方形的顶点重合),连接AE ,过点E作EF⊥AE交CD于点F.设BE=x,CF=y,求下列问题:
,过点E作EF⊥AE交CD于点F.设BE=x,CF=y,求下列问题:
(1)证明△ABE∽△ECF;
(2)求出y关于x的函数关系式;
(3)试求当x取何值时?y有最大或最小值,是多少?
 ,过点E作EF⊥AE交CD于点F.设BE=x,CF=y,求下列问题:
,过点E作EF⊥AE交CD于点F.设BE=x,CF=y,求下列问题:(1)证明△ABE∽△ECF;
(2)求出y关于x的函数关系式;
(3)试求当x取何值时?y有最大或最小值,是多少?
(1)证明:∵正方形ABCD,
∴∠B=∠C,∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠BEA+∠CEF=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF.
(2)∵△ABE∽△ECF,
∴
=
∵BE=x,CF=y,正方形ABCD的边长为1,
则CE=1-x,
∴
=
,
∴y=-x2+x.
(3)由(2)得y=-x2+x,
∴y=-(x-
)2+
,
∴可知抛物线的顶点为(
,
),开口向下,
∴x=
时,y最大=
.
∴∠B=∠C,∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠BEA+∠CEF=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF.
(2)∵△ABE∽△ECF,
∴
| AB |
| CE |
| BE |
| CF |
∵BE=x,CF=y,正方形ABCD的边长为1,
则CE=1-x,
∴
| 1 |
| 1-x |
| x |
| y |
∴y=-x2+x.
(3)由(2)得y=-x2+x,
∴y=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
∴可知抛物线的顶点为(
| 1 |
| 2 |
| 1 |
| 4 |
∴x=
| 1 |
| 2 |
| 1 |
| 4 |

练习册系列答案
相关题目


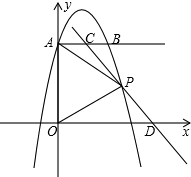 P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.

 在,请说明理由;
在,请说明理由;