题目内容
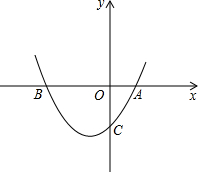
如图,在平面直角坐标系中,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为( )
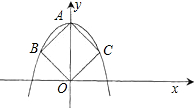
| A.1 | B.-1 | C.2 | D.-2 |

令x=0,得A点坐标(0,mc),
因为四边形ABOC为正方形,知∠AOC=45°,
所以c点坐标为:(
,
),
代入得:
=a×
+mc,
左右两边都除以
mc得:amc+2=0,
又有ac=-2,
∴m=1.
故选A.
因为四边形ABOC为正方形,知∠AOC=45°,
所以c点坐标为:(
| mc |
| 2 |
| mc |
| 2 |
代入得:
| mc |
| 2 |
| m2c2 |
| 4 |
左右两边都除以
| 1 |
| 4 |
又有ac=-2,
∴m=1.
故选A.

练习册系列答案
相关题目
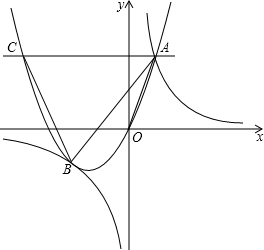

 x2)且(x1+1)(x2+1)=5
x2)且(x1+1)(x2+1)=5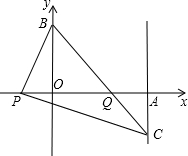 接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)
接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)