题目内容
如图,抛物线y=
x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的坐标是(1,0),点B的坐标是(-3,0).
(1)求m、n的值;
(2)求直线PC的解析式.
[温馨提示:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
,
)].
| 1 |
| 2 |
(1)求m、n的值;
(2)求直线PC的解析式.
[温馨提示:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |

(1)设抛物线的解析式为y=
(x+3)(x-1)=
x2+x-
,
所以m=1,n=-
;
(2)∵y=
x2+x-
,
∴C点坐标为(0,-
),
∵A的坐标是(1,0),点B的坐标是(-3,0),
∴抛物线的对称为直线x=-1,
把x=-1代入y=
x2+x-
得y=
-1-
=-2,
∴P点坐标为(-1,-2),
设直线PC的解析式为y=kx+b,
把P(-1,-2)、C(0,-
)代入得
,解得
∴直线PC的解析式为y=
x-
.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以m=1,n=-
| 3 |
| 2 |
(2)∵y=
| 1 |
| 2 |
| 3 |
| 2 |
∴C点坐标为(0,-
| 3 |
| 2 |
∵A的坐标是(1,0),点B的坐标是(-3,0),
∴抛物线的对称为直线x=-1,
把x=-1代入y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴P点坐标为(-1,-2),
设直线PC的解析式为y=kx+b,
把P(-1,-2)、C(0,-
| 3 |
| 2 |
|
|
∴直线PC的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 出它们的坐标;如果没有,说明理由.
出它们的坐标;如果没有,说明理由.
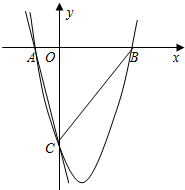 象经过A、C两点,且与x轴交于点B.
象经过A、C两点,且与x轴交于点B.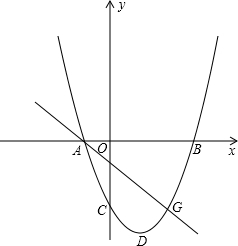 x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.