题目内容
如图,已知平面直角坐标系中三点A(2,0),B(0,2),P(x,0)(x<0),连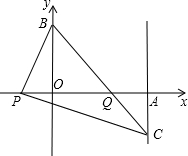 接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)
接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)
(1)求y与x之间的函数关系式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标.
 接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)
接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)(1)求y与x之间的函数关系式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标.
(1)∵PC⊥PB,BO⊥PO
∴∠CPA+∠OPB=90°,∠PBO+∠OPB=90°
∴∠CPA=∠PBO
∵A(2,0),C(2,y)在直线a上
∴∠BOP=∠PAC=90°
∴△BOP∽△PAC
∴
=
,
∴
=
,
∵x<0,y<0,
∴
=
∴y=-
x2+x.
(2)∵x<0,
∴x的最大整数值为-1
当x=-1时,y=-
,
∴C点的坐标为(2,-
);
设直线BC的解析式为y=kx+2,将C点坐标代入后可得:
2k+2=-
,k=-
,
因此直线BC的解析式为y=-
x+2.
当y=0时,0=-
x+2,x=
.
因此Q点的坐标为(
,0).
∴∠CPA+∠OPB=90°,∠PBO+∠OPB=90°
∴∠CPA=∠PBO
∵A(2,0),C(2,y)在直线a上
∴∠BOP=∠PAC=90°
∴△BOP∽△PAC
∴
| PO |
| AC |
| BO |
| PA |
∴
| |x| |
| |y| |
| 2 |
| |x|+2 |
∵x<0,y<0,
∴
| x |
| y |
| 2 |
| 2-x |
∴y=-
| 1 |
| 2 |
(2)∵x<0,
∴x的最大整数值为-1
当x=-1时,y=-
| 3 |
| 2 |
∴C点的坐标为(2,-
| 3 |
| 2 |
设直线BC的解析式为y=kx+2,将C点坐标代入后可得:
2k+2=-
| 3 |
| 2 |
| 7 |
| 4 |
因此直线BC的解析式为y=-
| 7 |
| 4 |
当y=0时,0=-
| 7 |
| 4 |
| 8 |
| 7 |
因此Q点的坐标为(
| 8 |
| 7 |

练习册系列答案
相关题目


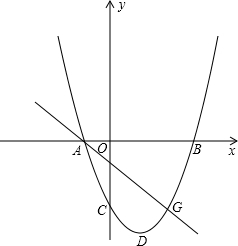 x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.