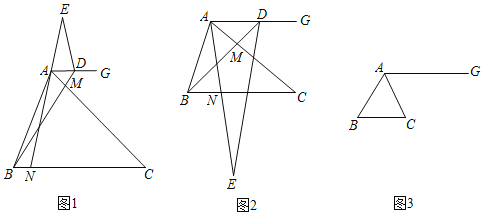
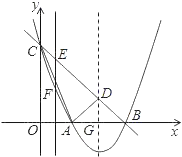
题目内容
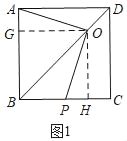
【题目】如图,正方形ABCD边长为4,点O在对角线DB上运动(不与点B,D重合),连接OA,作OP⊥OA,交直线BC于点P.
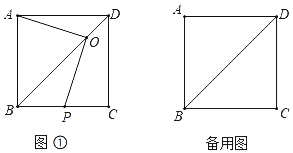
(1)判断线段OA,OP的数量关系,并说明理由.
(2)当OD=![]() 时,求CP的长.
时,求CP的长.
(3)设线段DO,OP,PC,CD围成的图形面积为S1,△AOD的面积为S2,求S1﹣S2的最大值.
【答案】(1)OA=OP,理由见解析;(2)PC=2;(3)当x=2时,S1﹣S2有最大值是4
【解析】
(1)证明四边形OGBH是正方形,得BG=BH,∠GOH=90°,再证明△AGO≌△PHO(ASA),则OA=OP;
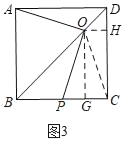
(2)如图2,作辅助线,证明△ODQ是等腰直角三角形,得OQ=DQ=1,证明△ADO≌△CDO(SAS),可得PC的长;
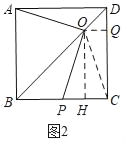
(3)如图3,作辅助线,构建三角形全等,设OH=x,则DH=x,CH=OG=4﹣x,PC=2x,根据S△AOD=S△COD,则S1﹣S2=S△POC=![]() =﹣x2+4x,配方后可得结论.
=﹣x2+4x,配方后可得结论.
解:(1)OA=OP,理由是:
如图1,过O作OG⊥AB于G,过O作OH⊥BC于H,
∵四边形ABCD是正方形,
∴∠ABO=∠CBO,AB=BC,
∴OG=OH,
∵∠OGB=∠GBH=∠BHO=90°,
∴四边形OGBH是正方形,
∴BG=BH,∠GOH=90°,
∵∠AOP=∠GOH=90°,
∴∠AOG=∠POH,
∴△AGO≌△PHO(ASA),
∴OA=OP;
(2)如图2,过O作OQ⊥CD于Q,过O作OH⊥BC于H,连接OC,
∴∠OQD=90°,
∵∠ODQ=45°,
∴△ODQ是等腰直角三角形,
∵OD=![]() ,
,
∴OQ=DQ=1,
∵AD=CD,∠ADO=∠CDO,OD=OD,
∴△ADO≌△CDO(SAS),
∴AO=OC=OP,
∵OH⊥PC,
∴PH=CH=OQ=1,
∴PC=2;
(3)如图3,连接OC,过O作OG⊥BC于G,OH⊥CD于H,
设OH=x,则DH=x,CH=OG=4﹣x,PC=2x,
由(2)知:△AOD≌△COD,
∴S△AOD=S△COD,
∴S1﹣S2=S1﹣S△COD=S△POC=![]() =﹣x2+4x=﹣(x﹣2)2+4,
=﹣x2+4x=﹣(x﹣2)2+4,
当x=2时,S1﹣S2有最大值是4.

 阅读快车系列答案
阅读快车系列答案【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.