��Ŀ����
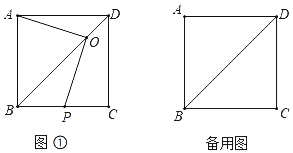
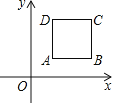
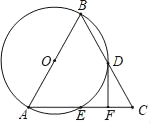
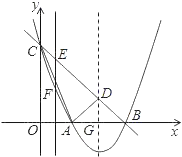
����Ŀ����ͼ����������Ϊ��2����1����������y��ax2+bx+c��a��0����y�ύ�ڵ�C��0��3������x�ύ��A��B���㣮
��1���������ߵı���ʽ��
��2���������ߵĶԳ�����ֱ��BC���ڵ�D������AC��AD�����ACD�������
��3����EΪֱ��BC��һ���㣬����E��y���ƽ����EF���������߽��ڵ�F�����Ƿ���ڵ�E��ʹ����D��E��FΪ��������������BCO���ƣ������ڣ����E�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y==x2-4x+3��
��2��AS��ACD=2��
��3���١�DFE=90��ʱ��E1��2+![]() ,1-
,1-![]() ��; E2��2-
��; E2��2-![]() ,1+
,1+![]() �����ڡ�EDF=90��ʱ��E3��1��2����E4��4��-1����
�����ڡ�EDF=90��ʱ��E3��1��2����E4��4��-1����
��������
��1����֪�����ߵĶ��㣬���Ƚ������ߵĽ���ʽ��Ϊ����ʽ���ٽ���C�������������Ľ���ʽ�У�����ȷ������ϵ����ֵ���ɴ˵ý⣮
��2���������A��C��D�������꣬�����ACD�����߳����жϳ��������ε���״�������õ��������ε��������Ҳ�ɽ���ACD�������Ϊ����������Сֱ�������ε�����
��3������ֱ��EF��y��ƽ�У���ô��OCB=��FED������OBC�͡�EFD���ƣ����EFD�У���EDF�͡�EFD�б���һ����ֱ�ǣ��ɾݴ������F�ĺ����꣬�ٴ���ֱ��BC�Ľ���ʽ�У����������E�����꣮
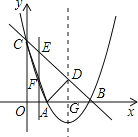 �⣺��1�������⣬�������ߵĽ���ʽΪ y=a��x-2��2-1������C��O��3���ã�
�⣺��1�������⣬�������ߵĽ���ʽΪ y=a��x-2��2-1������C��O��3���ã�
a��0-2��2-1=3��a=1
�������ߵĽ���ʽ��y=��x-2��2-1=x2-4x+3��
��2���ɣ�1��֪��A��1��0����B��3��0����
��ֱ��BC�Ľ���ʽΪ��y=kx+3�������B������ã�
3k+3=0��k=-1
��ֱ��BC��y=-x+3��
�ɣ�1��֪�������ߵĶԳ��x=2���� D��2��1����
��AD=![]() =
=![]() ��AC=
��AC=![]() =
=![]() ��CD=
��CD=![]() =2
=2![]() ��
��
����AC2=AD2+CD2����ACD��ֱ�������Σ���AD��CD��
��S��ACD=![]() ADCD=
ADCD=![]() ��
��![]() ��2
��2![]() =2��
=2��
��3��������֪��EF��y�ᣬ���FED=��OCB������OCB���FED���ƣ����У�
�١�DFE=90�㣬�� DF��x�
����D��������������ߵĽ���ʽ�У��ã�
x2-4x+3=1����� x=2��![]() ��
��
��x=2+![]() ʱ��y=-x+3=1-
ʱ��y=-x+3=1-![]() ��
��
��x=2-![]() ʱ��y=-x+3=1+
ʱ��y=-x+3=1+![]() ��
��
��E1��2+![]() ��1-
��1-![]() ����E
����E![]() ��1+
��1+![]() ����
����
�ڡ�EDF=90�㣻
��֪��ֱ��AD��y=x-1�����������ߵĽ���ʽ�У�
x2-4x+3=x-1��
x2-5x+4=0��
��� x1=1��x2=4��
��x=1ʱ��y=-x+3=2��
��x=4ʱ��y=-x+3=-1��
��E3��1��2����E4��4��-1����
���ϣ����ڷ��������ĵ�E��������Ϊ����2+![]() ��1-
��1-![]() ������2-
������2-![]() ��1+
��1+![]() ������1��2����4��-1����
������1��2����4��-1����
���㾦��������Ҫ�����˺�������ʽ��ȷ����ͼ������Ľⷨ�Լ����������ε��ж������ʵ�֪ʶ����Ҫע����ǣ���֪��������������ʱ������Ӧ�߲���ͬ����ô�õ��Ľ���Ͳ�һ����ͬ������һ��Ҫ���з������ۣ�

 ��У����ϵ�д�
��У����ϵ�д�