题目内容
【题目】已知△ABC中,CA=CB,0°<∠ACB≤90°,点M、N分别在边CA,CB上(不与端点重合),BN=AM,射线AG∥BC交BM延长线于点D,点E在直线AN上,EA=ED.
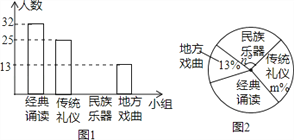
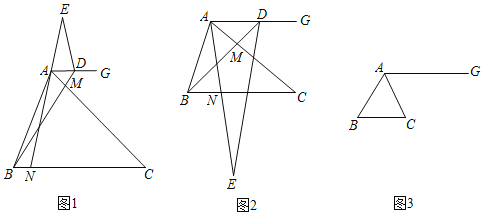
(1)(观察猜想)如图1,点E在射线NA上,当∠ACB=45°时,①线段BM与AN的数量关系是 ; ②∠BDE的度数是 ;
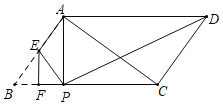
(2)(探究证明)如图2点E在射线AN上,当∠ACB=30°时,判断并证明线段BM与AN的数量关系,求∠BDE的度数;
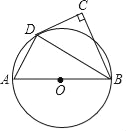
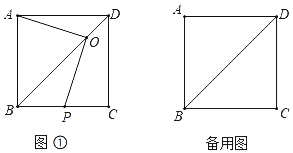
(3)(拓展延伸)如图3,点E在直线AN上,当∠ACB=60°时,AB=3,点N是BC边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.
【答案】(1)①BM=AN,②135°;(2)∠BDE=30°;(3)![]() 或4
或4
【解析】
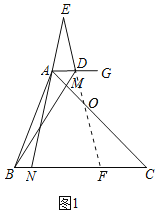
(1)如图1中,延长ED交BC于点F,交AC于点O.想办法证明∠BMC=∠BFE,再利用三角形的外角的性质即可解决问题;
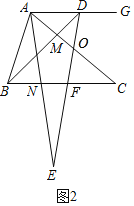
(2)如图2中,设AC交DF于点O.解决问题的方法类似(1);
(3)分两种情形分别画出图形,利用相似三角形的性质解决问题即可.
(1)如图1中,延长ED交BC于点F,交AC于点O,
∵CB=CA,
∴∠ABN=∠BAM,
∵BN=AM,AB=BA,
∴△ABN≌△BAM(SAS),
∴BM=AN,∠ANB=∠AMB,
∴∠ANC=∠BMC,
∵EA=ED,
∴∠EAD=∠EDA,
∵AG∥BC,
∴∠EAD=∠ENF,∠EDA=∠EFN,
∴∠BMC=∠BFE,
∴∠MOD+∠BDF=∠C+∠FOC,
∵∠C=45°,∠FOC=∠MOD,
∴∠MDO=45°,
∴∠BDE=135°,
故答案为BM=AN,135°.
(2)如图2中,设AC交DF于点O.
∵CB=CA,
∴∠ABN=∠BAM,
∵BN=AM,AB=BA,
∴△ABN≌△BAM(SAS),
∴BM=AN,∠ANB=∠AMB,
∴∠ANC=∠BMC,
∵EA=ED,
∴∠EAD=∠EDA,
∵AG∥BC,
∴∠EAD=∠ENF,∠EDA=∠EFN,
∴∠BMC=∠BFE,
∴∠MOD+∠BDF=∠C+∠FOC,
∵∠C=30°,∠FOC=∠MOD,
∴∠MDO=30°,
∴∠BDE=30°.
(3)①如图3﹣1中,
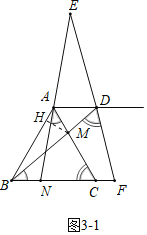
当BN=![]() BC时,作MH⊥AB于H,
BC时,作MH⊥AB于H,
由题意AM=BN=1,
在Rt△AHM中,∵∠MAH=60°.AM=1,
∴AH=![]() ,BH=
,BH=![]() ,HM=
,HM=![]() ,
,
在Rt△BMH中,BM=AN=DF=![]() ,
,
由(2)可知:∠BDF=∠ACB=60°,
∵∠CBM=∠DBF,
∴△CBM∽△DBF,
∴![]() ,
,
∴![]() ,
,
∴BF=![]() ,
,
∴CF=![]() ﹣3=
﹣3=![]() .
.
②如图3﹣2中,

当CN=![]() BC时,同法可得CF=4.
BC时,同法可得CF=4.
综上所述,满足条件的CF的长为![]() 或4.
或4.

 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】2019年3月30日,四川省凉山州木里县境内发生森林火灾,30名左右的扑火英雄牺牲,让人感到痛心,也再次给我们的防火安全意识敲响警钟.为了加强学生的防火安全意识,某校举行了一次“防火安全知识竞赛”(满分100分),赛后从中抽取了部分学生的成绩进行整理,并制作了如下不完整的统计图表:
组别 | 成绩x/分 | 组中值 |
A | 50≤x<60 | 55 |
B | 60≤x<70 | 65 |
C | 70≤x<80 | 75 |
D | 80≤x<90 | 85 |
E | 90≤x<100 | 95 |
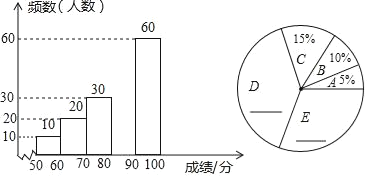
请根据图表提供的信息,解答下列各题:
(1)补全频数分布直方图和扇形统计图;
(2)分数段80≤x<90对应扇形的圆心角的度数是 °,所抽取的学生竞赛成绩的中位数落在 区间内;
(3)若将每组的组中值(各组两个端点的数的平均数)代表各组每位学生的竞赛成绩,请你估计该校参赛学生的平均成绩.