题目内容
【题目】永康市某校在课改中,开设的选修课有:篮球,足球,排球,羽毛球,乒乓球,学生可根据自己的爱好选修一门,李老师对九(1)班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
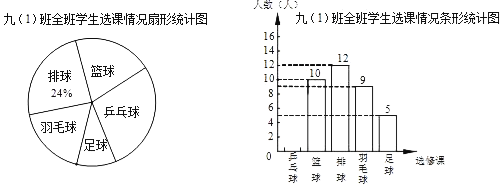
(1)该班共有学生 人,并补全条形统计图;
(2)求“篮球”所在扇形圆心角的度数;
(3)九(1)班班委4人中,甲选修篮球,乙和丙选修足球,丁选修排球,从这4人中任选2人,请你用列表或画树状图的方法,求选出的2人中恰好为1人选修篮球,1人选修足球的概率.
【答案】(1)50,图形见解析;(2)72°;(3)![]()
【解析】
(1)用排球的人数除以它所占的百分比即可得到全班人数,用总人数减去其它选课的人数求出乒乓球的人数,从而补全统计图;
(2)用篮球的所占百分比乘以360°即可得到在扇形统计图中“篮球”对应扇形的圆心角的度数;
(3)先画树状图展示所有12种等可能的结果数,找出选出的2人恰好1人选修篮球,1人选修足球所占结果数,然后根据概率公式求解.
(1)该班共有学生![]() (人),
(人),
乒乓球有50﹣10﹣12﹣9﹣5=14(人),
补图如下:
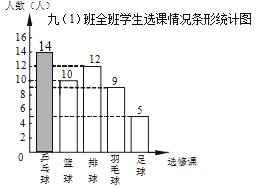
故答案为:50;
(2)![]() ;
;
(3)根据题意画图如下:用A表示篮球,用B表示足球,用C表示排球;
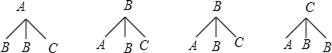
共有12种等可能的结果数,其中选出的2人恰好1人选修篮球,1人选修足球占4种,
所以选出的2人恰好1人选修篮球,1人选修足球的概率
所求的概率为![]() .
.

【题目】2019年3月30日,四川省凉山州木里县境内发生森林火灾,30名左右的扑火英雄牺牲,让人感到痛心,也再次给我们的防火安全意识敲响警钟.为了加强学生的防火安全意识,某校举行了一次“防火安全知识竞赛”(满分100分),赛后从中抽取了部分学生的成绩进行整理,并制作了如下不完整的统计图表:
组别 | 成绩x/分 | 组中值 |
A | 50≤x<60 | 55 |
B | 60≤x<70 | 65 |
C | 70≤x<80 | 75 |
D | 80≤x<90 | 85 |
E | 90≤x<100 | 95 |
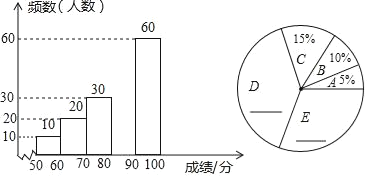
请根据图表提供的信息,解答下列各题:
(1)补全频数分布直方图和扇形统计图;
(2)分数段80≤x<90对应扇形的圆心角的度数是 °,所抽取的学生竞赛成绩的中位数落在 区间内;
(3)若将每组的组中值(各组两个端点的数的平均数)代表各组每位学生的竞赛成绩,请你估计该校参赛学生的平均成绩.