��Ŀ����
����Ŀ����ͼ���б߳�Ϊa�������ο�Ƭ�٣��߳�Ϊb�������ο�Ƭ�ڣ����ڱ߳��ֱ�Ϊa��b�ľ��ο�Ƭ�������ţ�
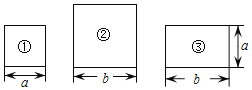
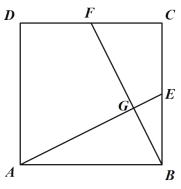
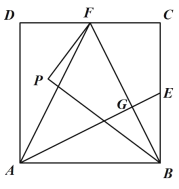
��1������2�ſ�Ƭ�٣�1�ſ�Ƭ�ڣ�3�ſ�Ƭ��ƴ��һ�����Σ��ڷ����л���������εIJ�ͼ��
��2������ƴͼǰ�����֮��Ĺ�ϵд��һ����ʽ��
��3��С���������Ʒ������Ͷ���ʽ�˷���a+3b����2a+2b���Ľ������ô���ÿ�Ƭ��______�ţ���Ƭ��______�ţ���Ƭ��______�ţ�
���𰸡���1��ͼ����ͼ����������2�����ݣ�a+3b����2a+2b��=2a2+8ab+6b2��
��3��2��6��8��
��������
��1������������Ƴ�ͼ�Σ������εij��Ϳ�Ϊ����Ϊ2a+b����Ϊa+b.
��2����ƴ��֮ǰ���������������ͼ�ε����֮������ʾ��ƴ��֮�����������ó����ε��������ʾ������ƴ��ǰ��������ȼ��ɵõ���ʽ.
��3�����ݵ�ʽ��֪ƴ�Ϻ�ij����εij���Ϊa+3b��2a+2b��Ȼ����Ƴ�ͼ�μ��ɽ����.
��1���������⣬��֪ͼ�����£�
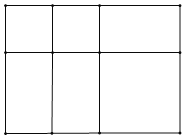
��2��ƴ��ǰ�����Ϊ2a2+3ab+b2
ƴ�Ϻ�����Ϊ��a+b����2a+b����
����ƴ��ǰ�������ȣ��ɵ�2a2+3ab+b2=��a+b����2a+b��
��3�����ݣ�a+3b����2a+2b��=2a2+8ab+6b2����֪ƴ�Ϻ�ij����εij���Ϊa+3b��2a+2b����˿ɻ��Ƴ�ͼ�����£�

��ô���ÿ�Ƭ��2�ţ���Ƭ��6�ţ���Ƭ��8�ţ�
�ʴ�Ϊ2��6��8��

 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д� Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�