��Ŀ����
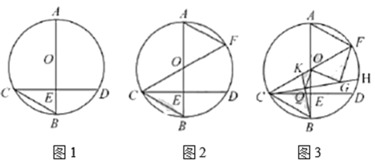
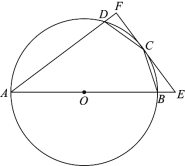
����Ŀ����ͼ����ƽ��ֱ�������У�������y��ax2+bx+c����A����1��0����B��3��0����C��0��3������P��ֱ��BC�Ϸ��������ϵ�һ���㣬PE��y�ᣬ��ֱ��BC�ڵ�E����AP����ֱ��BC�ڵ� D��
��1���������ߵĺ�������ʽ��
��2����AD��2PDʱ�����P�����ꣻ
��3�����߶�PE�����ֵ��
��4�����߶�PE���ʱ������F��ֱ��BC���ҡ�EFP��2��ACO��ֱ��д����F�����꣮

���𰸡���1��y����x2+2x+3����2��P��1��4����P��2��3������3������![]() ����
����![]() ��
��
��������
��1��������������x�����������������֪���ɰ������ߵĽ���ʽ��ɽ���ʽ���ٴ�����һ��֪���������������ʽ��
��2����A��EF��x�ᣬ��BC�ཻ�ڵ�F���ô���ϵ�������BC�Ľ���ʽ����P��ĺ�����Ϊt���������AF��PE�������������εı����߶����t��ɣ�
��3������PE����t�ĺ�������ʽ���ɺ�����������������ֵ��ɣ�
��4��������������ٵ�F����PE�����ʱ������P��PM��BC�ڵ�M����E��EN��x���ڵ�N������F��FQ��x���ڵ�Q������O��OG��AC�ڵ�G��ȡAC���е�H������OH��ͨ���������������MF��ֵ��ɣ��ڽ���õ�F�����꣬����PM�ԳƵ������һF�㣮
��1���������ߵĽ���ʽΪ��y��a��x+1����x��3����a��0����
��3��a��1������3����
��a����1��
�������ߵĽ���ʽΪ��y������x+1����x��3����
��y����x2+2x+3��
��2����A��EF��x�ᣬ��BC�ཻ�ڵ�F����ͼ1����P��t����t2+2t+3����
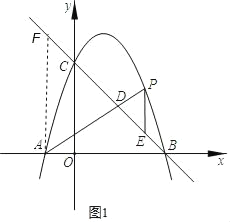
��AF��PE��
��BC�Ľ���ʽΪy��kx+b��k��0����
��![]() ��
��
���![]() ��
��
��ֱ��BC�Ľ���ʽΪ��y����x+3��
��E��t����t+3����F����1��4����
��AF��4��PE����t2+3t��
��AF��PE��
���AFD�ס�PED��
��![]() ��
��
��AD��2PD��
��![]() ��
��
��ã�t��1��2��
��P��1��4����P��2��3����
��3����PE�Ľ���ʽΪ��PE����t2+3t������t��![]() ��2+
��2+![]() ��0��t��3����
��0��t��3����
�൱t��![]() ʱ��PE��ֵ���Ϊ
ʱ��PE��ֵ���Ϊ![]() ��
��
��4���ٵ�F����PE�����ʱ��
����P��PM��BC�ڵ�M����E��EN��x���ڵ�N������F��FQ��x���ڵ�Q������O��OG��AC�ڵ�G��ȡAC���е�H������OH��
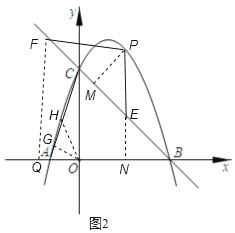
�ɣ�3��֪����PEȡ���ֵʱ��P��![]() ��
��![]() ����PE��
����PE��![]() ��E��
��E��![]() ��
��![]() ����
����
��OB��OC��3��
���OBC����OCB��45����
��BE��![]() EM��
EM��![]() ����PEM��45����
����PEM��45����
��PM��EM��![]() ��
��
��AC��![]() ��
��
��OH��CH��![]() ��
��
OG��![]() ��
��
��HG��![]() ����OHG��2��ACO��
����OHG��2��ACO��
�ߡ�EFP��2��ACO��
���EFP����OHG��
�ߡ�OGH����PMF��
���OGH�ס�PMF��
��![]() ����
����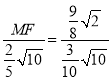 ��
��
��MF��![]() ��
��
��BF��BE+EM+MF��![]() ��
��
��FQ��BQ��![]() BF��
BF��![]() ��
��
��OQ��![]() ��
��
��F����![]() ��
��![]() ����
����
�ڵ�F����PE���ұ�ʱ����ʱ��F��ǡ���루��![]() ��
��![]() ������PM�Գƣ������ʱF��
������PM�Գƣ������ʱF��![]() ��
��![]() ����
����
��F����������![]() ��
��![]() ����
����![]() ��
��![]() ����
����

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�����Ŀ��ij�̳��ס��ҡ�������ҵ��Ա2018��ǰ5���µ����۶��λ����Ԫ�����±���
�·� ���۶� ��Ա | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
�� | 6 | 9 | 10 | 8 | 8 |
�� | 5 | 7 | 8 | 9 | 9 |
�� | 5 | 9 | 10 | 5 | 11 |
��1�������ϱ��е����ݣ����±�����������
ͳ��ֵ ��ֵ ��Ա | ƽ��������Ԫ�� | ��������Ԫ�� | ��λ������Ԫ�� | ���� |
�� | 8 | 8 | 1.76 | |
�� | 7.6 | 8 | 2.24 | |
�� | 8 | 5 |
��2���ס��ҡ�������ҵ��Ա��˵�Լ�������ҵ���ã�����ͬ˭��˵������˵������.