Question

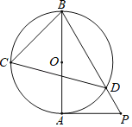
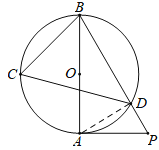
【题目】如图AB是⊙O的直径，PA与⊙O相切于点A，BP与⊙O相交于点D，C为⊙O上的一点，分别连接CB、CD，∠BCD＝60°．

(1)求∠ABD的度数；

(2)若AB＝6，求PD的长度．

Answer 1

【答案】（1）∠ABD=30°；（2）PD=．

【解析】

（1）根据圆周角定理得：∠ADB=90°，由同弧所对的圆周角相等和直角三角形的性质可得结论；

（2）如图1，根据切线的性质可得∠BAP=90°，根据直角三角形30°角的性质可计算AD的长，由勾股定理计算DB的长，由三角函数可得PB的长，从而得PD的长．

（1）如图，连接AD．

∵BA是⊙O直径，

∴∠BDA=90°．

∵，

∴∠BAD=∠C=60°．

∴∠ABD=90°-∠BAD=90°-60°=30°．

（2）如图，∵AP是⊙O的切线，

∴∠BAP=90°．

在Rt△BAD中，∵∠ABD=30°，

∴DA=BA=×6=3．

∴BD=DA=3．

在Rt△BAP中，∵cos∠ABD=，

∴cos30°=．

∴BP=4．

∴PD=BP-BD=4-3=．