题目内容
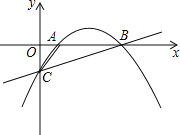
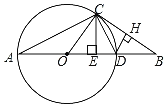
【题目】如图,O是![]() ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.
ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.
(1)求证:直线BC是⊙O的切线;
(2)若⊙O的半径为3,CD=2,求BC的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明∠OCD+∠DCB=90°,得出∠OCB=90°,则结论得证;
(2)证明△CDB∽△ACB,得出![]() ,设BC=x,则AB=2
,设BC=x,则AB=2![]() x,DB=2
x,DB=2![]() x﹣6,由BC2=ABDB得出方程,解方程则可得出答案.
x﹣6,由BC2=ABDB得出方程,解方程则可得出答案.
(1)证明:∵CE⊥AB,
∴∠CED=90°,
∴∠ECD+∠CDE=90°,
∵OC=DO,
∴∠ODC=∠OCD,
∵CD平分∠BCE,
∴∠ECD=∠DCB,
∴∠OCD+∠DCB=90°,
∴∠OCB=90°,
∴直线BC是⊙O的切线;
(2)∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD+∠CDA=90°,
∵∠DCB+∠ODC=90°,
∴∠DCB=∠CAD,
∵∠CBD=∠ABC,
∴△CDB∽△ACB,
∴![]() ,
,
∴BC2=ABDB
∵⊙O的半径为3,CD=2,
∴AC=![]() =
=![]() =4
=4![]() ,
,
∴![]() =
=![]() ,
,
设BC=x,则AB=2![]() x,DB=2
x,DB=2![]() x﹣6,
x﹣6,
∴x2=2![]() ,
,
解得x=![]() ,
,
∴BC=![]() .
.

 口算小状元口算速算天天练系列答案
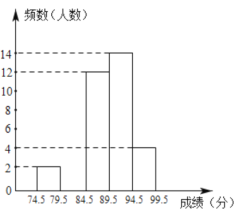
口算小状元口算速算天天练系列答案【题目】某校开展“祖国在我心中”主题演讲比赛,参加选拔比赛的选手的成绩(满分为![]() 分),分成五组,制成了如下不完整的统计图表.
分),分成五组,制成了如下不完整的统计图表.
分数段 | 频数 | 频率 |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
(1)求分数在![]() 参赛学生的频率;
参赛学生的频率;
(2)求分数在![]() 参赛学生的频数,并补全频数分布直方图;
参赛学生的频数,并补全频数分布直方图;
(3)成绩在![]() 分以上的选手中,有三名男生和一名女生,学校从中随机确定
分以上的选手中,有三名男生和一名女生,学校从中随机确定![]() 名选手参加市级比赛,求恰好是一名男生和一名女生的概率.
名选手参加市级比赛,求恰好是一名男生和一名女生的概率.
【题目】新冠肺炎疫情发生后,口罩市场出现热销,小明的爸爸用12000元购进医用外科、N95两种型号的口罩在自家药房销售,销售完后共获利2700元,进价和售价如下表:
品名价格 | 医用外科口罩 | N95口罩 |
进价(元/袋) | 20 | 30 |
售价(元/袋) | 25 | 36 |
(1)小明爸爸的药房购进医用外科、N95两种型号口罩各多少袋?
(2)该药房第二次以原价购进医用外科、N95两种型号口罩,购进医用外科口罩袋数不变,而购进N95口罩袋数是第一次的2倍,医用外科口罩按原售价出售,而效果更好的N95口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋N95口罩最多打几折?