题目内容
【题目】在正方形![]() 中,点
中,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() .
.
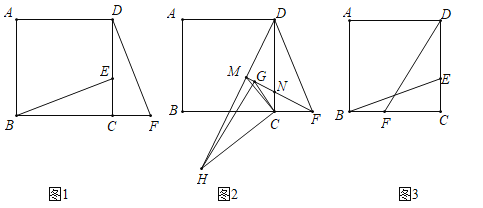
(1)如图1,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
①求证:![]() ;
;
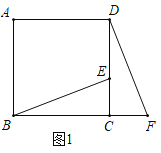
②如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到对应
得到对应![]() ,射线
,射线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
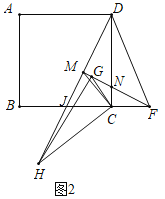
(2)如图3,若![]() ,点
,点![]() 是
是![]() 边上的动点,且
边上的动点,且![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
【答案】(1)①详见解析;②详见解析;(2)![]()
【解析】
(1)①欲证明DF=BE,只要证明△BCE≌△DCF(SAS)即可.
②证明△DCJ∽△FMJ,推出![]() ,推出△JMC∽△JFD,可得
,推出△JMC∽△JFD,可得![]() ,推出DF=2CM可得结论.
,推出DF=2CM可得结论.
(2)如图3中,连接AE,延长BC到T,使得CT=BC,连接AT.想办法证明DF=AE,BE=ET,推出DF+BE=AE+ET.根据AE+ET≥AT,利用勾股定理求出AT即可解决问题.
(1)①证明:如图1中,
∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠DCF=90°,
∵CE=CF,
∴△BCE≌△DCF(SAS),
∴BE=DF.
②解:结论:HG=2CM.
理由:如图2中,设DH交BC于J.
∵∠DCG=30°,∠DCF=90°,
∴∠GCF=120°,
∵CG=CF,
∴∠CFG=∠CGF=30°,
∵CD=CH,∠DCH=120°,
∴∠CDH=∠CHD=30°,
∵∠DCJ=90°,
∴∠DJC=60°,DJ=2CJ
∴∠JMF=90°,
∵∠DJC=∠FJM,∠DCJ=∠FMJ,
∴△DCJ∽△FMJ,
∴![]() ,
,
∵∠MJC=∠FJD,
∴△JMC∽△JFD,
∴![]() ,
,
∴DF=2CM,
∵HG=DF,
∴HG=2CM.
(2)如图3中,连接AE,延长BC到T,使得CT=BC,连接AT.
∵四边形ABCD是正方形,
∴AD=DC,∠ADE=∠DCF=∠ABT=90°,
∵CF+CE=2=CD=CE+DE,
∴DE=CF,
∴△ADE≌△DCF(SAS),
∴AE=DF,
∵CD⊥BT,CB=CT,
∴EB=ET,
∴DF+BE=AE+ET,
∵AE+ET≥AT,AT=![]() ,
,
∴DF+BE=AE+ET≥![]() ,
,
∴DF+BE的最小值为![]() .
.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案