题目内容
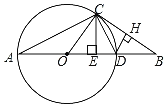
【题目】如图,抛物线y=ax2+bx﹣![]() 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.
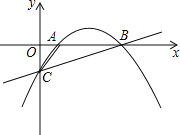
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]()
![]() +2x﹣
+2x﹣![]() ;(2)
;(2)![]() ;(3)存在最大值,此时P点坐标(
;(3)存在最大值,此时P点坐标(![]() ,
,![]() ).
).
【解析】
(1)将A、B两点坐标分别代入抛物线解析式,可求得待定系数a和b,即可确定抛物线解析式;(2)因为圆的切线垂直于过切点的半径,所以过A作AD⊥BC于点D,则AD为⊙A的半径,由条件可证明△ABD∽△CBO,根据抛物线解析式求出C点坐标,根据勾股定理求出BC的长,再求出AB的长,利用相似三角形的性质即两个三角形相似,对应线段成比例,可求得AD的长,即为⊙A的半径;(3)先由B,C点坐标求出直线BC解析式,然后过P作PQ∥y轴,交直线BC于点Q,交x轴于点E,因为P在抛物线上,P,Q点横坐标相同,所以可设出P、Q点的坐标,并把PQ的长度表示出来,进而表示出△PQC和△PQB的面积,两者相加就是△PBC的面积,再利用二次函数的性质讨论其最大值,容易求得P点坐标.
解:(1)∵抛物线y=ax2+bx﹣![]() 经过点A(1,0)和点B(5,0),
经过点A(1,0)和点B(5,0),
∴把A、B两点坐标代入可得: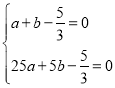 ,
,
解得: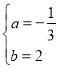 ,
,
∴抛物线解析式为y=﹣![]()
![]() +2x﹣
+2x﹣![]() ;
;
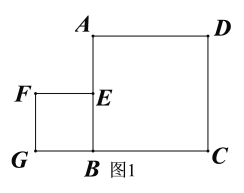
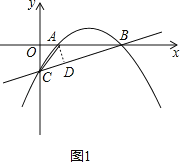
(2)过A作AD⊥BC于点D,
如图1:因为圆的切线垂直于过切点的半径,所以AD为⊙A的半径,
由(1)可知C(0,﹣![]() ),且A(1,0),B(5,0),
),且A(1,0),B(5,0),
∴OB=5,AB=OB﹣OA=4,OC=![]() ,
,
在Rt△OBC中,由勾股定理可得:BC=![]() =
=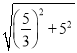 =
=![]() ,∵∠ADB=∠BOC=90°,∠ABD=∠CBO,
,∵∠ADB=∠BOC=90°,∠ABD=∠CBO,
∴△ABD∽△CBO,
∴![]() ,即
,即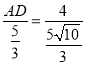 ,
,
解得AD=![]() ,
,
即⊙A的半径为![]() ;
;
(3)∵C(0,﹣![]() ),
),
∴设直线BC解析式为y=kx﹣![]() ,
,
把B点坐标(5,0)代入可求得k=![]() ,
,
∴直线BC的解析式为y=![]() x﹣
x﹣![]() ,
,
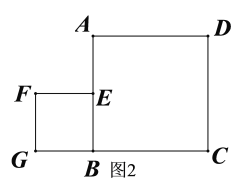
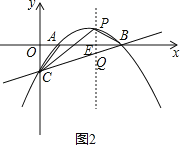
过P作PQ∥y轴,交直线BC于点Q,交x轴于点E,
如图2,因为P在抛物线上,Q在直线BC上,P,Q两点横坐标相同,
所以设P(x,﹣![]()
![]() +2x﹣
+2x﹣![]() ),
),
则Q(x,![]() x﹣
x﹣![]() ),
),
∴PQ=(﹣![]()
![]() +2x﹣
+2x﹣![]() )﹣(
)﹣(![]() x﹣
x﹣![]() )=﹣
)=﹣![]()
![]() +
+![]() x=﹣
x=﹣![]()
![]() +
+![]() ,∴S△PBC=S△PCQ+S△PBQ
,∴S△PBC=S△PCQ+S△PBQ
=![]() PQOE+
PQOE+![]() PQBE=
PQBE=![]() PQ(OE+BE)
PQ(OE+BE)
=![]() PQOB=
PQOB=![]() PQ
PQ
=![]() ×[﹣
×[﹣![]()
![]() +
+![]() ]
]
=![]() ,
,
∵![]() <0,∴当x=
<0,∴当x=![]() 时,S△PBC有最大值
时,S△PBC有最大值![]() ,
,
把x=![]() 代入﹣
代入﹣![]()
![]() +2x﹣
+2x﹣![]() ,
,
求出P点纵坐标为![]() ,
,
∴△PBC的面积存在最大值,此时P点坐标(![]() ,
,![]() ).
).

 综合自测系列答案
综合自测系列答案