Question

【题目】如图所示，已知抛物线y=x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标；

(2)若点C在抛物线上，且点C的横坐标为8，求四边形AMBC的面积.

Answer 1

【答案】（1）M（2，-3）；（2）36

【解析】

（1）用待定系数法即可解得抛物线的解析式及顶点M的坐标；

（2）先求出点C的坐标，再用面积相加的方法求得四边形AMBC的面积.

解：（1）将点A（-1,0）、点B（5,0）代入y=x2+bx+c中，得

可得 ，

解得 ，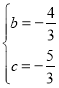

所以抛物线的解析式为y = - - ，

化为顶点式为y = -3

故点M（2，-3）

（2）代入x=8，可得y=9

故C（8,9）

因为AB=5+1=6，

且△ABM、△ABC的高分别是点M、点C纵坐标的绝对值，

所以S四边形AMBC=S△ABM+S△ABC= + =36.