题目内容
【题目】在平面直角坐标系中,我们将抛物线![]() 通过平移后得到
通过平移后得到![]() ,且设平移后所得抛物线的顶点依次为
,且设平移后所得抛物线的顶点依次为![]() ,这些顶点均在格点上,我们将这些抛物线称为“缤纷抛物线”(k为整数).
,这些顶点均在格点上,我们将这些抛物线称为“缤纷抛物线”(k为整数).
(1)![]() 的坐标为____________,直接写出平移后抛物线
的坐标为____________,直接写出平移后抛物线![]() 的解析式为____________(用k表示);
的解析式为____________(用k表示);
(2)若平移后的抛物线![]() 与抛物线
与抛物线![]() 交于点A,对称轴与抛物线
交于点A,对称轴与抛物线![]() 交于点B,若
交于点B,若![]() ,求整数k的值.
,求整数k的值.
【答案】(1)(6,12),![]() ;(2)4或
;(2)4或![]() .
.
【解析】
(1)观察平移后抛物线顶点坐标的特点,然后依据规律即可得到平移后抛物线![]() 的解析式;
的解析式;
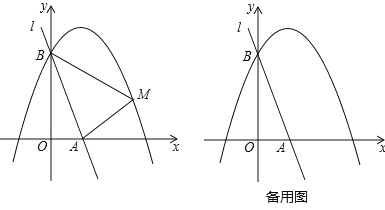
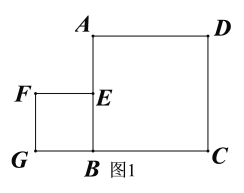
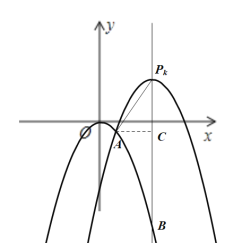
(2)如图1所示:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由
,由![]() 可知顶点
可知顶点![]() ,对称轴为
,对称轴为![]() ,对称轴与抛物线
,对称轴与抛物线![]() 的交点为
的交点为![]() ,然后求得抛物线的交点
,然后求得抛物线的交点![]() ,
,![]() ,最后依据
,最后依据![]() 列方程求解即可;
列方程求解即可;
解:(1)![]() 抛物线
抛物线![]() 通过平移后得到
通过平移后得到![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 的坐标为:(6,12),
的坐标为:(6,12),
∴![]() ;
;
(2)如图1所示:过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
由![]() 可知顶点
可知顶点![]() ,对称轴为
,对称轴为![]() ,对称轴与抛物线
,对称轴与抛物线![]() 的交点为
的交点为![]() ,
,
解![]() 得
得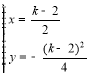 ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() 即
即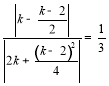 ,整理得:
,整理得:![]() ,
,
解得![]() 或
或![]() 或
或![]() ;
;
当![]() 时原方程无意义,故
时原方程无意义,故![]() 不是原方程的根.
不是原方程的根.
![]() 的值为4或
的值为4或![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目