题目内容
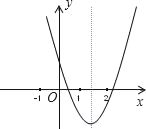
【题目】如图,在平面直角坐标系中抛物线y=(x+1)(x﹣3)与x轴相交于A、B两点,若在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,则m的值是( )
A. 6 B. 8 C. 12 D. 16
【答案】B
【解析】
根据题目中的函数解析式可以求得该抛物线与x轴的交点坐标和顶点的坐标,再根据在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,可知其中一点一定在顶点处,从而可以求得m的值.
∵抛物线y=(x+1)(x-3)与x轴相交于A、B两点,
∴点A(-1,0),点B(3,0),该抛物线的对称轴是直线x=![]() =1,
=1,
∴AB=3-(-1)=4,该抛物线顶点的纵坐标是:y=(1+1)×(1-3)=-4,
∵在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,
∴m=![]() =8,
=8,
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目