题目内容
【题目】如图,在同一平面内,两条平行的高速公路AB和CD之间有一条“L”型道路连通,“L”型道路中的EP=FP=20千米,∠BEP=12°,∠EPF=80°,求AB和CD之间的距离.(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
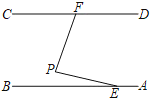
【答案】22.2(km)
【解析】
过P作MN⊥AB于M,交CD于N,根据平行线的性质和解直角三角形的方法即可得到结论.
解:过P作MN⊥AB于M,交CD于N,

∵AB∥CD,
∴MN⊥CD,
∴∠FNP=∠PME=90°,
∵∠BEP=20°,PE=20,
∴PM=PEsin∠PEM=20×0.21=4.2(千米),
∵∠EPM=90°﹣12°=78°,∠EPF=80°,
∴∠FPN=22°,
∴PN=PFcos∠FPN=20×0.93=18.3,
∴AB和CD之间的距离=PM+PN=4.2+18.3=22.2(km).

练习册系列答案
相关题目