题目内容
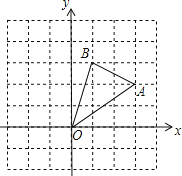
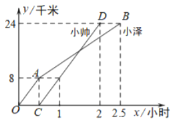
【题目】如图所示抛物线
过点
，点
，且
（1）求抛物线的解析式及其对称轴；
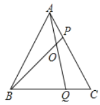
（2）点
在直线
上的两个动点，且
，点
在点
的上方，求四边形
的周长的最小值；
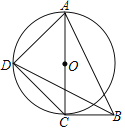
（3）点
为抛物线上一点，连接
，直线把四边形
的面积分为3∶5两部分，求点的坐标.
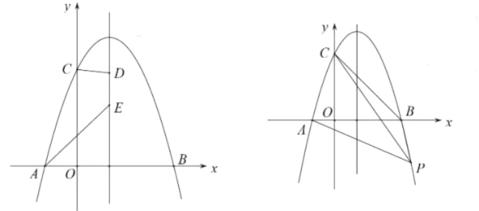
【答案】（1）
，对称轴为直线
；（2）四边形
的周长最小值为
；（3）
【解析】
（1）OB=OC，则点B（3，0），则抛物线的表达式为：y=a（x+1）（x-3）=a（x2-2x-3）=ax2-2ax-3a，即可求解；
（2）CD+AE=A′D+DC′，则当A′、D、C′三点共线时，CD+AE=A′D+DC′最小，周长也最小，即可求解；
（3）S△PCB：S△PCA=
EB×（yC-yP）：AE×（yC-yP）=BE：AE，即可求解．
（1）∵OB=OC，∴点B（3，0），
则抛物线的表达式为：y=a（x+1）（x-3）=a（x2-2x-3）=ax2-2ax-3a，
故-3a=3，解得：a=-1，
故抛物线的表达式为：y=-x2+2x+3…①；
对称轴为：直线
（2）ACDE的周长=AC+DE+CD+AE，其中AC=
、DE=1是常数，
故CD+AE最小时，周长最小，
取点C关于函数对称点C（2，3），则CD=C′D，
取点A′（-1，1），则A′D=AE，
故：CD+AE=A′D+DC′，则当A′、D、C′三点共线时，CD+AE=A′D+DC′最小，周长也最小，
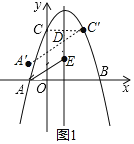
四边形ACDE的周长的最小值=AC+DE+CD+AE=+1+A′D+DC′=+1+A′C′=+1+
；
（3）如图，设直线CP交x轴于点E，
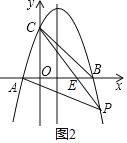
直线CP把四边形CBPA的面积分为3：5两部分，
又∵S△PCB：S△PCA=EB×（yC-yP）：AE×（yC-yP）=BE：AE，
则BE：AE，=3：5或5：3，
则AE=
或
，
即：点E的坐标为（，0）或（，0），
将点E、C的坐标代入一次函数表达式：y=kx+3，
解得：k=-6或-2，
故直线CP的表达式为：y=-2x+3或y=-6x+3…②
联立①②并解得：x=4或8（不合题意值已舍去），
故点P的坐标为（4，-5）或（8，-45）．
【题目】水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性，进行了抽样调查，从甲、乙两个大棚各收集了 24 株秧苗上的小西红柿的个数，并对数据进行整理、描述和分析。
下面给出了部分信息：（说明：45 个以下为产量不合格，45 个及以上为产量合格，其中 45～65 个为产量良好，65～85 个为产量优秀）
a.补全下面乙组数据的频数分布直方图(数据分成 6 组: 25≤x＜35，35≤x＜45，45≤x＜55，55≤x＜65，65≤x＜75，75≤x＜85):
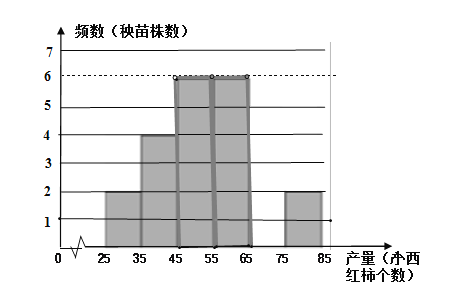
b.乙组数据在产量良好（45≤x＜65）这两组的具体数据为： 46 46 47 47 48 48 55 57 57 57 58 61
c.数据的平均数、众数和方差如下表所示：
大棚 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 52.25 | 51 | 58 | 238 |
乙 | 52.25 | 57 | 210 |
（1）补全乙的频数分布直方图.
（2）写出表中
的值．
（3）根据样本情况，估计乙大棚产量良好及以上的秧苗数为 株．
（4）根据抽样调查情况，可以推断出 大棚的小西红柿秧苗品种更适应市场需求，写出理由．（至少从两个不同的角度说明推断的合理性）．
【题目】某体育用品商店购进了足球和排球共20个，一共花了1360元，进价和售价如表：
足球 | 排球 | |
进价（元/个） | 80 | 50 |
售价（元/个） | 95 | 60 |
（l）购进足球和排球各多少个？
（2）全部销售完后商店共获利润多少元？
