题目内容
【题目】![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
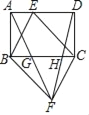
(1)如图1,求证:![]() ;
;
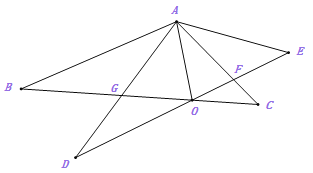
(2)如图2,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
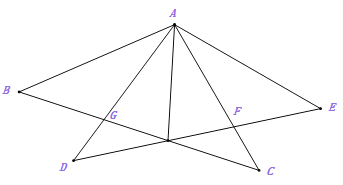
(3)若![]() ,
,![]() 交
交![]() 于
于![]() ,且
,且![]() 为等腰三角形,则
为等腰三角形,则![]() ______.
______.
【答案】(1)见解析;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)只要证明△ABC≌△ADE(SAS)即可解决问题;
(2)过A作AM⊥BC于M,作AN⊥DE于N,想办法证明△ABO≌△AEO(ASA)即可解决问题;
(3)分两种情形讨论即可解决问题;
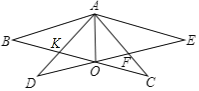
(1)证明:设AD交OB于K.
在△ABC和△ADE中
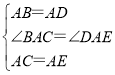 ,
,
∴△ABC≌△ADE(SAS),
∴∠B=∠D,
∵∠AKB=∠DKO,
∴∠BOD=∠BAD=α
(2)过A作AM⊥BC于M,作AN⊥DE于N
∵△ABC≌△ADE,
∴S△ABC=S△ADE,
∴![]() BCAM=
BCAM=![]() DEAN,
DEAN,
∵BC=DE,
∴AM=AN
∴AO平分∠BOE,
∵AO平分∠DAC,
∴∠DAO=∠CAO,
∴∠BAO=∠EAO
在△ABO和△AEO中,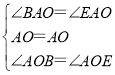 ,
,
∴△ABO≌△AEO(ASA)
∴AB=AE,
∵AB=AD,AC=AE,
∴AC=AD,
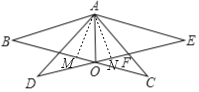
(3)由(2)可知∠AOB=∠AOF,
∴∠AOF≠∠OAF(否则CA∥CB),
∴只有AO=AF或OA=OF,
①当AO=AF时,∠AOF=∠AFO=∠AOB=α+30°,
∴∠AOB+∠AOF+∠FOC=180°,
∴2(α+30)+α=180°,
∴α=40°.
②当OA=OF时,∠OAF=∠OFA=α+30°,
∴∠AOB=∠AOF=180°-2(α+30°),
∴2[180°-2(α+30)]+α=180°,
∴α=20°,
综上所述,α=40°或20°

练习册系列答案
相关题目