题目内容
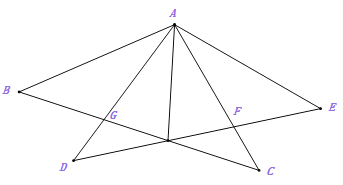
【题目】如图，点E是矩形ABCD边AD上的一个动点，且与点A、点D不重合，连结BE、CE，过点B作BF∥CE，过点C作CF∥BE，交点为F点，连接AF、DF分别交BC于点G、H，则下列结论错误的是（ ）
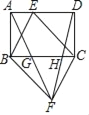
A. GH=
BC B. S△BGF+S△CHF=
S△BCF
C. S四边形BFCE=ABAD D. 当点E为AD中点时，四边形BECF为菱形
【答案】B
【解析】
根据矩形的性质、平行四边形的判定和性质一一判断即可；
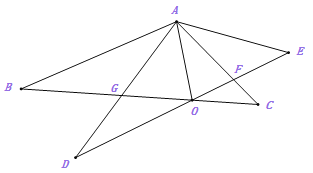
连接EF交BC于O．
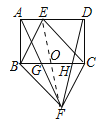
∵BF∥CE，CF∥BE，∴四边形BECF是平行四边形，∴EO=OF．
∵GH∥AD，∴AG=GF，HD=FH，∴GH=
AD=BC．故选项A正确．
∵BG+CH=GH，∴S△BGF+S△CHF=S△BCF．
故选项B错误．
∵S四边形BFCE=2S△EBC=2××BC×AB=BC×AB=ABAD．故选项C正确．
∵当点E为AD中点时，易证EB=EC，所以四边形BECF为菱形．故选项D正确．
故选B．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
