Question

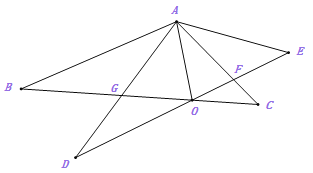
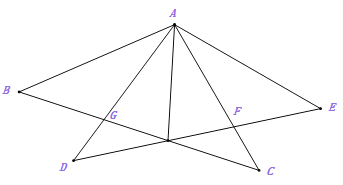
【题目】如图，已知△ABC三个内角的平分线交于点O，延长BA到点D，使AD=AO，连接DO，若BD=BC，∠ABC=54，则∠BCA的度数为________．

Answer 1

【答案】42°

【解析】

试题由△ABC三个内角的平分线得到角相等，关键等腰三角形的性质得到∠D=∠AOD，由外角的性质得到∠BAC=4∠D，由△DBO≌△CBO，得到∠BOC=∠D=α，∠BCA=2α，根据三角形的内角和列方程求得．

试题解析：∵△ABC三个内角的平分线交于点O，

∴∠ABO=∠CBO，∠BAO=∠CAO，∠BCO=∠ACO，

∵AD=A0，

∴∠D=∠AOD，

∴∠BAO=2∠D，

设∠D=α，

则∠BAO=2α，∠BAC=4α，

在△DBO与△CBO中，

∴△DBO≌△CBO，

∴∠BOC=∠D=α，

∴∠BCA=2α，

∴54+4α+2α=180，

∴α=21，

∴∠BCA=42°