题目内容
【题目】问题情境：综合实践活动课上，同学们围绕“已知三角形三边的长度，求三角形的面积”开展活动，启航小组同学想到借助正方形网格解决问题
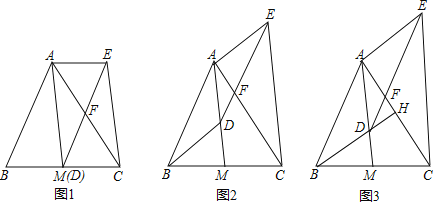
问题解决：图（1）、图（2）都是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，操作发现，启航小组同学在图（1）中画出△ABC，其顶点A，B，C都在格点上，同时构造长方形CDEF，使它的顶点都在格点上，且它的边EF经过点A，ED经过点B．同学们借助此图求出了△ABC的面积．
（1）在图（1）中，△ABC的三边长分别是AB＝ ，BC＝ ，AC＝ ．△ABC的面积是 ．
（2）已知△PMN中，PM＝
，MN＝2
，NP＝
．请你根据启航小组的思路，在图（2）中画出△PMN，并直接写出△RMN的面积 ．
【答案】（1）
，
，
，
；（2）图见解析；7．
【解析】
（1）利用勾股定理求出AB，BC，AC，理由分割法求出△ABC的面积．
（2）模仿（1）中方法，画出△PMN，利用分割法求解即可．
解：（1）如图1中，AB＝
＝
＝，BC＝
＝
＝，AC＝
＝
＝，
S△ABC＝S矩形DEFC﹣S△AEB﹣S△AFC﹣S△BDC＝12﹣3﹣
﹣2＝，
故答案为，，，．
（2）△PMN如图所示．
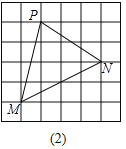
S△PMN＝4×4﹣2﹣3﹣4＝7，
故答案为7．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
