题目内容
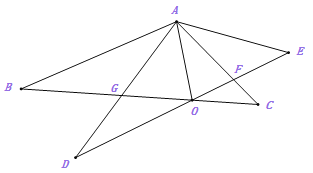
【题目】如图1，在Rt△ADE中，∠DAE=90°，C是边AE上任意一点（点C与点A、E不重合），以AC为一直角边在Rt△ADE的外部作Rt△ABC，∠BAC=90°，连接BE、CD．
（1）在图1中，若AC=AB，AE=AD，现将图1中的Rt△ADE绕着点A顺时针旋转锐角α，得到图2，那么线段BE．CD之间有怎样的关系，写出结论，并说明理由；
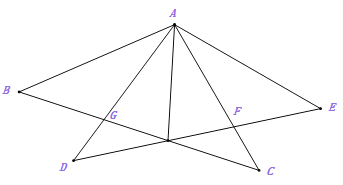
（2）在图1中，若CA=3，AB=5，AE=10，AD=6，将图1中的Rt△ADE绕着点A顺时针旋转锐角α，得到图3，连接BD、CE．
①求证：△ABE∽△ACD；
②计算：BD2+CE2的值．
【答案】（1）BE=CD，BE⊥CD，理由见角；（2）①证明见解析；②BD2+CE2=170．
【解析】
（1）结论：BE=CD，BE⊥CD；只要证明△BAE≌△CAD，即可解决问题；
（2）①根据两边成比例夹角相等即可证明△ABE∽△ACD．
②由①得到∠AEB=∠CDA．再根据等量代换得到∠DGE=90°，即DG⊥BE，根据勾股定理得到BD2+CE2=CB2+ED2，即可根据勾股定理计算．
（1）结论：BE=CD，BE⊥CD．
理由：设BE与AC的交点为点F，BE与CD的交点为点G，如图2．
∵∠CAB=∠EAD=90°，∴∠CAD=∠BAE．
在△CAD和△BAE中，∵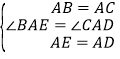
，∴△CAD≌△BAE，∴CD=BE，∠ACD=∠ABE．
∵∠BFA=∠CFG，∠BFA+∠ABF=90°，∴∠CFG+∠ACD=90°，∴∠CGF=90°，∴BE⊥CD．
（2）①设AE与CD于点F，BE与DC的延长线交于点G，如图3．
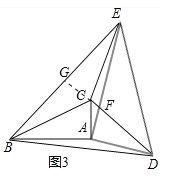
∵∠CABB=∠EAD=90°，∴∠CAD=∠BAE．
∵CA=3，AB=5，AD=6，AE=10，∴
=
=2，∴△ABE∽△ACD；
②∵△ABE∽△ACD，∴∠AEB=∠CDA．
∵∠AFD=∠EFG，∠AFD+∠CDA=90°，∴∠EFG+∠AEB=90°，∴∠DGE=90°，∴DG⊥BE，∴∠AGD=∠BGD=90°，∴CE2=CG2+EG2，BD2=BG2+DG2，∴BD2+CE2=CG2+EG2+BG2+DG2．
∵CG2+BG2=CB2，EG2+DG2=ED2，∴BD2+CE2=CB2+ED2=CA2+AB2+AD2+AD2=170．
