题目内容
【题目】如图①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)请你判断并写出FE与FD之间的数量关系(不需证明);
(2)如图②,如果∠ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

【答案】(1)FE=FD (2)答案见解析
【解析】
(1)先在AC上截取AG=AE,连结FG,利用SAS判定△AEF≌△AGF,得出∠AFE=∠AFG,FE=FG,再利用ASA判定△CFG≌△CFD,得到FG=FD,进而得出FE=FD;
(2)先过点F分别作FG⊥AB于点G,FH⊥BC于点H,则∠FGE=∠FHD=90°,根据已知条件得到∠GEF=∠HDF,进而判定△EGF≌△DHF(AAS),即可得出FE=FD.也可以过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,再判定△EFG≌△DFH(ASA),进而得出FE=FD.
(1)FE与FD之间的数量关系为:FE=FD.
理由:如图,在AC上截取AG=AE,连结FG,
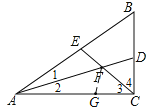
∵AD是∠BAC的平分线,
∴∠1=∠2,
在△AEF与△AGF中
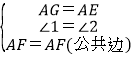 ,
,
∴△AEF≌△AGF(SAS),
∴∠AFE=∠AFG,FE=FG,
∵∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,
∴2∠2+2∠3+∠B=180°,
∴∠2+∠3=60°,
又∵∠AFE为△AFC的外角,
∴∠AFE=∠CFD=∠AFG=∠2+∠3=60°,
∴∠CFG=180°-60°-60°=60°,
∴∠GFC=∠DFC,
在△CFG与△CFD中,
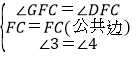 ,
,
∴△CFG≌△CFD(ASA),
∴FG=FD,
∴FE=FD;
(2)结论FE=FD仍然成立.
如图,过点F分别作FG⊥AB于点G,FH⊥BC于点H,则∠FGE=∠FHD=90°,
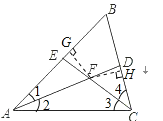
∵∠B=60°,且AD,CE分别是∠BAC,∠BCA的平分线,
∴∠2+∠3=60°,F是△ABC的内心,
∴∠GEF=∠BAC+∠3=∠1+∠2+∠3=60°+∠1,
∵F是△ABC的内心,即F在∠ABC的角平分线上,
∴FG=FH,
又∵∠HDF=∠B+∠1=60°+∠1,
∴∠GEF=∠HDF,
在△EGF与△DHF中,
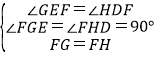 ,
,
∴△EGF≌△DHF(AAS),
∴FE=FD.

【题目】列方程解应用题
学校给七年级学生组织知识竞赛,共设20道题,各题的分值相同,每题必答.下表记录了5名学生的得分情况
参赛者 | 答对题数 | 答错题数 | 得分 |
小明 | 10 | 10 | 40 |
小红 | 19 | 1 | 94 |
小刚 | 20 | 0 | 100 |
小强 | 18 | 2 | 88 |
小丽 | 14 | 6 | 64 |
(1)参赛者小芳得76分,她答对了几道题?
(2)参赛者小花说她得了83分,你认为可能吗?为什么?