题目内容
【题目】已知:AB、CD 是圆O 的两条直径,且∠AOD =α(0° < α < 90°),点P是扇形AOD内任意一点.点P将AB、CD所在直线依次轮流作为对称轴翻折,将点P关于AB对称的点记为点P1 ,点P1关CD 对称的点记为点P2,点 P2 关于AB 对称的点记为点P3,….
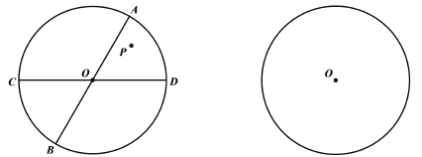
(1)根据所给图中点P 的位置,分别画出点 P 1、P 1;(不写作图步骤,但要保留作图痕迹)
(2)分别联结OP、OP1、OP2,那么线段OP、OP1、OP2 之间的数量关系是:OP OP1 OP2(填空,不要求写出过程);
(3)由(1)、(2)可知,点 P 绕点O旋转可以到达点P2的位置,如果 α=60°,OP= a,求线段 OP顺时针旋转到OP2 过程中扫过的面积;
(4)在 α 取某些特定值的时候,如果按照这样的方式翻折,总能得到一点Pn与点P 重合, 求当n =12,点 P12 与点P 第一次重合时 α 的值.(直接写出结果,不要求写出过程)
【答案】(1)见详解 (2)= = (3)![]() (4)
(4)![]()
【解析】
(1)见详解图;
(2)根据垂直平分线的性质可以知道都是相等的;
(3)根据转过的圆心角代入到扇形的面积公式,可以求出面积;
(4)根据题意可以得出答案,
解:(1)如图所示:

(2)如图所示:相等;

(3)如上图所示:
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() 到
到![]() 所扫过的角度为:
所扫过的角度为:![]() ,
,
且其扫过的面积为扇形![]() 的面积,
的面积,
![]() ;
;
(4)根据规律可得:
![]() ,
,
故![]() 与
与![]() 第一次重合时
第一次重合时![]() .
.

练习册系列答案
相关题目