题目内容
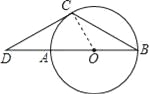
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)根据切线的判定方法,只需证CD⊥OC.所以连接OC,证∠OCD=90°;
(2)易求半径OC的长.在Rt△OCD中,运用三角函数求CD.
试题解析:(1)连接OC.
∵OB=OC,∠B=30°,
∴∠OCB=∠B=30°,
∴∠COD=∠B+∠OCB=60°,
∵∠BDC=30°,
∴∠BDC+∠COD=90°,DC⊥OC,
∵BC是弦,
∴点C在⊙O上,
∴DC是⊙O的切线,点C是⊙O的切点;
(2)解:∵AB=2,
∴OC=OB=![]() =1,
=1,
∵在Rt△COD中,∠OCD=90°,∠D=30°,
∴DC=![]() OC=
OC=![]() .
.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】呈贡区商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
![]() 进价、售价均保持不变,利润
进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本
进货成本![]()
![]() 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价;
![]() 若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?