Question

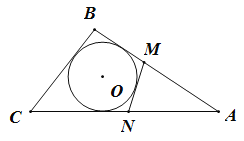
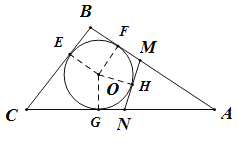
【题目】如图，△ABC周长为20cm，BC=6cm,圆O是△ABC的内切圆，圆O的切线MN与AB、CA相交于点M、N，则△AMN的周长为________cm.

Answer 1

【答案】8

【解析】

先作出辅助线,连接切点,利用内切圆的性质得到BE=BF,CE=CG,ME=MH,NG=NH,再利用等量代换即可解题.

解：∵圆O是△ABC的内切圆，MN是圆O的切线,

如下图,连接各切点,有切线长定理易得,

BE=BF,CE=CG,ME=MH,NG=NH,

∵△ABC周长为20cm, BC=6cm,

∴BC=CE+BE=CG+BF=6cm,

∴△AMN的周长=AM+AN+MN=AM+AN+FM+GN=AF+AG,

又∵AF+AG=AB+AC-(BF+CG)=20-6-6=8cm

故答案是8