题目内容
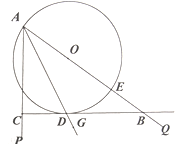
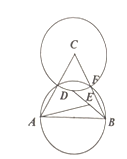
【题目】如图，已知等边△ABC的边长为4，以AB为直径的圆交BC于点F，CF为半径作圆，D是⊙C上一动点，E是BD的中点，当AE最大时，BD的长为（ ）
A.
B.
C.4D.6
【答案】B
【解析】
点E在以F为圆心的圆上运到，要使AE最大，则AE过F，根据等腰三角形的性质和圆周角定理证得F是BC的中点，从而得到EF为△BCD的中位线，根据平行线的性质证得CD⊥BC，根据勾股定理即可求得结论．
解：点D在⊙C上运动时，点E在以F为圆心的圆上运到，要使AE最大，则AE过F，
连接CD，
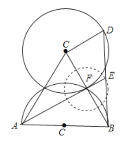
∵△ABC是等边三角形，AB是直径，
∴EF⊥BC，
∴F是BC的中点，
∵E为BD的中点，
∴EF为△BCD的中位线，
∴CD∥EF，
∴CD⊥BC，BC=4，CD=2，
故BD= 
，
故选：B．
练习册系列答案
相关题目
【题目】在学校组织的科学素养竞赛中，每班参加比赛的人数相同，成绩分为
、
、
、
四个等级，其中相应等级的得分依次为
分，
分，
分，
分.马老师将九年级一班和二班的成绩整理并绘制成如下的统计图：
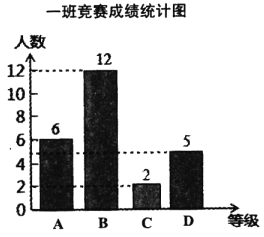
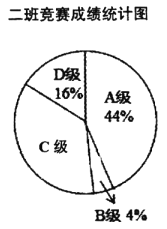
请你根据以上提供的信息解答下列问题：
（1）此次竞赛中二班成绩在分及其以上的人数是_______人；
（2）补全下表中
、
、
的值：
平均数（分） | 中位数（分） | 众数（分） | 方差 | |
一班 |
|
|
|
|
二班 |
|
|
|
|
（3）学校准备在这两个班中选一个班参加市级科学素养竞赛，你建议学校选哪个班参加？说说你的理由.