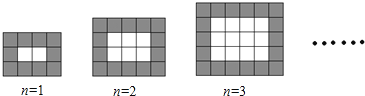
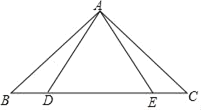
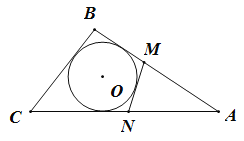
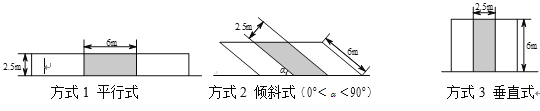
题目内容
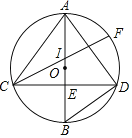
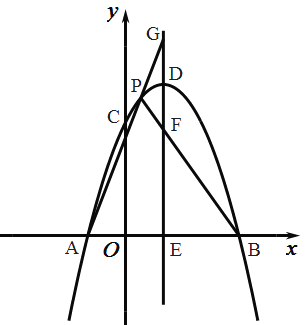
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点,OA=1,OB=3,抛物线的顶点坐标为D(1,4).
(1)求A、B两点的坐标;
(2)求抛物线的表达式;
(3)过点D做直线DE//y轴,交x轴于点E,点P是抛物线上A、D两点间的一个动点(点P不于A、D两点重合),PA、PB与直线DE分别交于点G、F,当点P运动时,EF+EG的值是否变化,如不变,试求出该值;若变化,请说明理由。
【答案】(1)(-1,0),(3,0);(2)![]() ;(3)8.
;(3)8.
【解析】
(1)根据OA,OB的长,可得答案;
(2)根据待定系数法,可得函数解析式;
(3)根据相似三角形的判定与性质,可得EG,EF的长,根据整式的加减,可得答案.
解:(1)由抛物线![]() 交
交![]() 轴于
轴于![]() 两点(A在B的左侧),且OA=1,OB=3,得A点坐标(-1,0),B点坐标(3,0);
两点(A在B的左侧),且OA=1,OB=3,得A点坐标(-1,0),B点坐标(3,0);
(2)设抛物线的解析式为![]() ,
,
把C点坐标代入函数解析式,得
![]()
解得![]() ,
,
抛物线的解析式为![]() ;
;
(3)EF+EG=8(或EF+EG是定值),理由如下:
过点P作PQ∥y轴交x轴于Q,如图:
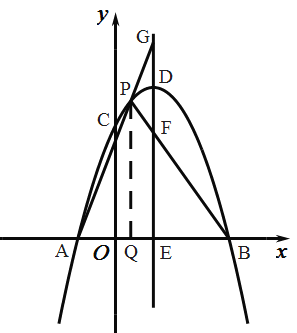
设P(t,-t2+2t+3),
则PQ=-t2+2t+3,AQ=1+t,QB=3-t,
∵PQ∥EF,
∴△BEF∽△BQP
∴![]()
∴![]()
又∵PQ∥EG,
∴△AEG∽△AQP,
∴![]()
∴![]()
∴![]() .
.

练习册系列答案
相关题目
【题目】小明将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系,y与x的几组对应值如下表所示:
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(Ⅰ)求y关于x的函数解析式(不要求写x的取值范围);
(Ⅱ)问:小球的飞行高度能否达到22m?请说明理由.