题目内容
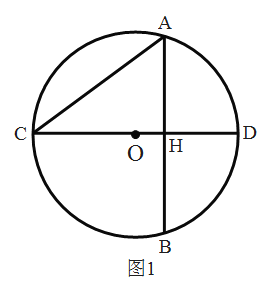
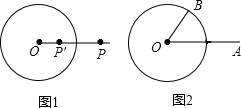
【题目】如图1,⊙O的半径为r,若点P′在射线OP上,满足OP′×OP=r2,则称点P′是点P关于⊙O的“反演点”,如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A'是点A关于⊙O的反演点,求A'B的长为( )
A.![]() B.2
B.2![]() C.2D.4
C.2D.4
【答案】B
【解析】
设OA交⊙O于C,连结BC,如图2,根据新定义计算出OA′=2,OB=4,则点A′为OC的中点,再证明△OBC为等边三角形,则BA′⊥OC,然后在Rt△OA′B中,利用正弦的定义可求A′B的长.
解:设OA交⊙O于C,连结B′C,如图2,
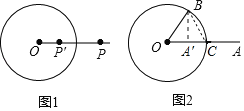
∵OA′OA=42
而r=4,OA=8
∴OA′=2,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴BA′⊥OC,
在Rt△OA′B中,sin∠A′OB=![]() ,
,
∴A′B=4sin60°=2![]() .
.
故选:B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
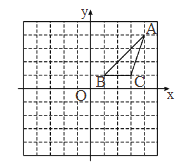
【题目】某公司从2016年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年度 | 投入技改资金x/万元 | 产品成本y/(万元/件) |
2016 | 2 | 18 |
2017 | 3 | 12 |
2018 | 4 | 9 |
2019 | 4.5 | 8 |
(1)根据表格中数据,求y关于x的函数解析式。
(2)在图中的网格中建立适当的平面直角坐标系,画出该函数的大致图像。
(3)如果打算在2020年让产品成本不高于7万元,则投入技改资金至少为 万元。