题目内容
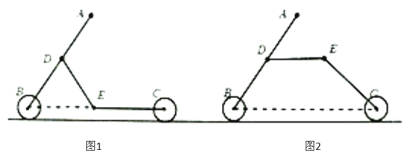
【题目】某工厂生产某种多功能儿童车，根据需要可变形为图1的滑板车或图2的自行车，已知前后车轮半径相同，
，
，车杆
与
所成的
，图1中
、
、
三点共线，图2中的座板
与地面保持平行.问变形前后两轴心的长度有没有发生变化？若不变，请写出的长度；若变化，请求出变化量？（参考数据：
，
，
）
【答案】
的长度发生了改变，减少了
.
【解析】
根据图形的特点构造直角三角形利用三角函数求出变化前BC与变化后的BC长度即可求解.
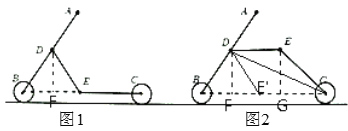
图1：作DF⊥BC于F点，∵
∴BF=EF=BDcos
≈30×
=18
∴BC=2BF+CE
图2：作DF⊥BC于F点，由图1可知∠DE’F=53°，
∴∠DE’C=180°-∠DE’F=127°
∵DE∥BC，
∴∠E’DE=∠DE’F=53°
根据题意可知DE’=DE,CE’=CE,
连接CD，∴△DCE≌△DCE’
∴∠DEC=∠DE’C=127°
∴∠ECB=360°-∠DEC-∠DE’C-∠E’DE=53°，
作EG⊥BC于G点
∴BC=BF+FG+GC= BDcos+DE+CE
∠ECB
30×+30+40×=
76-72=4cm，
答：的长度发生了改变，减少了.
优生乐园系列答案
【题目】某公司从2016年开始投入技术改进资金，经技术改进后，其产品的成本不断降低，具体数据如下表：
年度 | 投入技改资金x/万元 | 产品成本y/(万元/件) |
2016 | 2 | 18 |
2017 | 3 | 12 |
2018 | 4 | 9 |
2019 | 4.5 | 8 |
（1）根据表格中数据，求y关于x的函数解析式。
（2）在图中的网格中建立适当的平面直角坐标系，画出该函数的大致图像。
（3）如果打算在2020年让产品成本不高于7万元，则投入技改资金至少为 万元。
【题目】在学校组织的科学素养竞赛中，每班参加比赛的人数相同，成绩分为
、
、
、
四个等级，其中相应等级的得分依次为
分，
分，
分，
分.马老师将九年级一班和二班的成绩整理并绘制成如下的统计图：
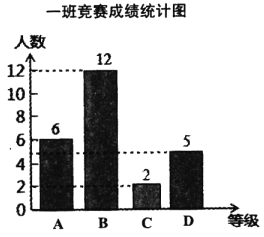
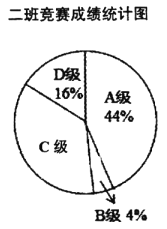
请你根据以上提供的信息解答下列问题：
（1）此次竞赛中二班成绩在分及其以上的人数是_______人；
（2）补全下表中
、
、
的值：
平均数（分） | 中位数（分） | 众数（分） | 方差 | |
一班 |
|
|
|
|
二班 |
|
|
|
|
（3）学校准备在这两个班中选一个班参加市级科学素养竞赛，你建议学校选哪个班参加？说说你的理由.
【题目】小明将小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系，y与x的几组对应值如下表所示：
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(Ⅰ)求y关于x的函数解析式(不要求写x的取值范围)；
(Ⅱ)问：小球的飞行高度能否达到22m？请说明理由.
