Question

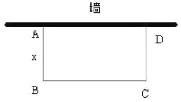
【题目】如图,园林小组的同学用一段长16米的篱笆围成一个一边靠墙的矩形菜园ABCD,墙的长度为9米,设AB的长为x米,BC的长为y米.

(1)①写出y与x的函数关系是: ;

②自变量x的取值范围是 ;

(2)园林小组的同学计划使矩形菜园的面积为30平方米,试求此时边AB的长.

Answer 1

【答案】（1）①y=16-2x②≤x<8（2）5米

【解析】

（1）由篱笆总长16米，可得y与x的函数关系；

（2）由x＞0，y＞0及y≤9可得x的取值范围；

（3）由矩形菜园的面积为30平方米，可列方程求得AB的长.

(1)①y=16-2x;

②≤x<8;

(2)由题意,AB·BC=x(16-2x)=30,

解得:x1=5,x2=3

x2=3不在(1)中x的取值范围内,故舍去.

答:此时边AB的长为5米.