Question

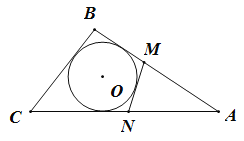
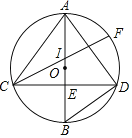
【题目】△ABC中，∠C=90°，内切圆与AB相切于点D，AD=2，BD=3，则△ABC的面积为（　　）

A.3B.6C.12D.无法确定

Answer 1

【答案】B

【解析】

易证得四边形OECF是正方形，然后由切线长定理可得AC=2+r，BC=3+r，AB=5，根据勾股定理列方程即可求得答案．

如图，设⊙O分别与边BC、CA相切于点E、F，

连接OE，OF，

∵⊙O分别与边AB、BC、CA相切于点D、E、F，
∴DE⊥BC，DF⊥AC，AF=AD=2，BE=BD=3，
∴∠OEC=∠OFC=90°，
∵∠C=90°，
∴四边形OECF是矩形，
∵OE=OF，
∴四边形OECF是正方形，
设EC=FC=r，
∴AC=AF+FC=2+r，BC=BE+EC=3+r，AB=AD+BD=2+3=5，
在Rt△ABC中，=+，
∴=+，
∴，
即
解得：或（舍去）．
∴⊙O的半径r为1,

∴．

故选：B