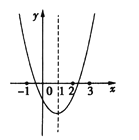
题目内容
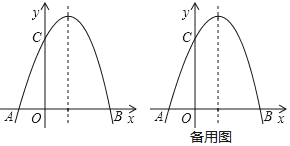
【题目】二次函数![]() 的图象如图,有下列结论:①
的图象如图,有下列结论:①![]() ,②
,②![]() ,③
,③![]() 时,
时,![]() ,④
,④![]() ,⑤当
,⑤当![]() 且
且![]() 时,
时,![]() ,⑥当
,⑥当![]() 时,
时,![]() .其中正确的有( )
.其中正确的有( )
A.①②③B.②④⑥C. ②⑤⑥D.②③⑤
【答案】D
【解析】
①只需根据抛物线的开口、对称轴的位置、与y轴的交点位置就可得到a、b、c的符号,从而得到abc的符号;②只需利用抛物线对称轴方程x=![]() =1就可得到2a与b的关系;③只需结合图象就可得到当x=1时y=a+b+c最小,从而解决问题;④根据抛物线x=
=1就可得到2a与b的关系;③只需结合图象就可得到当x=1时y=a+b+c最小,从而解决问题;④根据抛物线x=![]() 图象在x轴上方,即可得到x=
图象在x轴上方,即可得到x=![]() 所对应的函数值的符号;⑤由
所对应的函数值的符号;⑤由![]() 可得
可得![]() ,然后利用抛物线的对称性即可解决问题;⑥根据函数图像,即可解决问题.
,然后利用抛物线的对称性即可解决问题;⑥根据函数图像,即可解决问题.
解:①由抛物线的开口向下可得a>0,
由对称轴在y轴的右边可得x=![]() >0,从而有b<0,
>0,从而有b<0,
由抛物线与y轴的交点在y轴的负半轴上可得c<0,
则abc>0,故①错误;
②由对称轴方程x=![]() =1得b=-2a,即2a+b=0,故②正确;
=1得b=-2a,即2a+b=0,故②正确;
③由图可知,当x=1时,y=a+b+c最小,则对于任意实数m(![]() ),都满足
),都满足![]() ,即
,即![]() ,故③正确;
,故③正确;
④由图像可知,x=![]() 所对应的函数值为正,
所对应的函数值为正,
∴x=![]() 时,有a-b+c>0,故④错误;
时,有a-b+c>0,故④错误;
⑤若![]() ,且x1≠x2,
,且x1≠x2,
则![]() ,
,
∴抛物线上的点(x1,y1)与(x2,y2)关于抛物线的对称轴对称,
∴1-x1=x2-1,即x1+x2=2,故⑤正确.
⑥由图可知,当![]() 时,函数值有正数,也有负数,故⑥错误;
时,函数值有正数,也有负数,故⑥错误;
∴正确的有②③⑤;
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目