题目内容
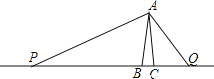
【题目】如图,在平面直角坐标系![]() 中,已知点A(1,2),B(3,2),连接AB. 若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
中,已知点A(1,2),B(3,2),连接AB. 若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
(1)在点C(0,2),D(2,![]() ),E(4,1)中,线段AB的“临近点”是__________;
),E(4,1)中,线段AB的“临近点”是__________;
(2)若点M(m,n)在直线![]() 上,且是线段AB的“临近点”,求m的取值范围;
上,且是线段AB的“临近点”,求m的取值范围;
(3)若直线![]() 上存在线段AB的“临近点”,求b的取值范围.
上存在线段AB的“临近点”,求b的取值范围.
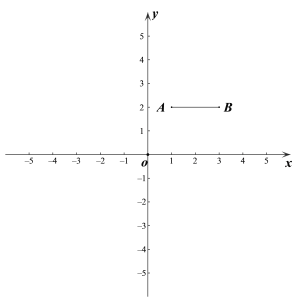
【答案】(1)C、D ;(2)0≤m≤![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据线段AB的“临近点”的定义解答即可;
(2)设![]() 与y轴交于M,与A2B2交于N,求出M的坐标和N的坐标,即可得出m的取值范围.
与y轴交于M,与A2B2交于N,求出M的坐标和N的坐标,即可得出m的取值范围.
(3)分别求出直线![]() 与半圆A相切、半圆B相切时b的值,即可得到结论.
与半圆A相切、半圆B相切时b的值,即可得到结论.
(1)∵A(1,2),C(0,2),∴AC=1.
∵A(1,2)在线段AB上,∴点C是线段AB的“临近点”;
∵点![]() 离线段AB上(2,2)点最近,2-
离线段AB上(2,2)点最近,2-![]() =
=![]() <1,∴点D是线段AB的“临近点”;
<1,∴点D是线段AB的“临近点”;
∵E(4,1)与线段AB上点B的距离最近,EB=![]() >1,∴点E不是线段AB的“临近点”.
>1,∴点E不是线段AB的“临近点”.
故线段AB的“临近点”是C、D .
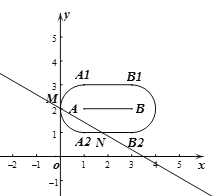
(2)如图,设![]() 与y轴交于M,与A2B2交于N,易知M(0,2),∴m≥0,易知N的纵坐标为1,代入
与y轴交于M,与A2B2交于N,易知M(0,2),∴m≥0,易知N的纵坐标为1,代入![]() ,可求横坐标为
,可求横坐标为![]() ,∴m≤
,∴m≤![]() ,∴0≤m≤
,∴0≤m≤![]() .
.
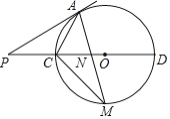
(3)如图2,设直线![]() 为l,令y=0,得:x=
为l,令y=0,得:x=![]() b.当直线
b.当直线![]() 与半圆A相切时,过A作AF⊥直线l于F,作AH⊥x轴于H,交直线l于点R,则∠FAR=∠RGH=30°.
与半圆A相切时,过A作AF⊥直线l于F,作AH⊥x轴于H,交直线l于点R,则∠FAR=∠RGH=30°.
∵A(1,2),∴OH=1,AH=2.
∵AF=1,∠FAR=30°,∴AR=![]() ,∴RH=AH-AR=2-
,∴RH=AH-AR=2-![]() .
.
在Rt△RHG中,∵∠RGH=30°,∴HG=![]() RH.
RH.
∵HG=OG-OH=![]() ,∴
,∴![]() =
=![]() ,解得:
,解得:![]() ;
;
当直线![]() 与半圆B相切时,类似可求:
与半圆B相切时,类似可求:![]() ;
;
∴![]() .
.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目