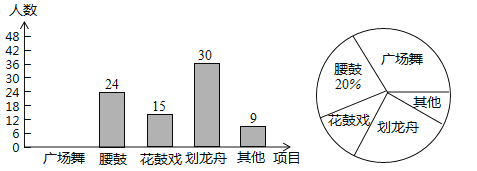
题目内容
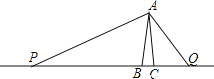
【题目】如图,在△ABC中,AB=AC=2,∠BAC=20°。动点P,Q分别在直线BC上运动,且始终保持∠PAQ=100°。设BP=x,CQ=y,求y与x之间的函数表达式。
【答案】![]()
【解析】
由AB=AC,∠BAC=20°,得∠ABC=80°,即∠P+∠PAB=80°,由∠BAC=20°,∠PAQ=100°,得∠PAB+∠QAC=80°,由此可得∠P=∠QAC,同理可证∠PAB=∠Q,从而证明△PAB∽△AQC,利用相似比求函数关系式.
∵AB=AC,∠BAC=20°,
∴∠ABC=(180°-∠BAC)÷2=80°,即 ∠P+∠PAB=80°,
又∵∠BAC=20°,∠PAQ=100°,
∴∠PAB+∠QAC=80°
∴∠P=∠QAC
同理,∠PAB=∠Q,
∴△PAB∽△AQC,
∴![]() ,即
,即![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目