题目内容
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
【答案】D
【解析】
先根据题意,画出图形,令直线y= ![]() x+
x+ ![]() 与x轴交于点C,与y轴交于点D,作OH⊥CD于H,作OH⊥CD于H;
与x轴交于点C,与y轴交于点D,作OH⊥CD于H,作OH⊥CD于H;
然后根据坐标轴上点的坐标特点,由一次函数解析式,求得C、D两点的坐标值;
再在Rt△POC中,利用勾股定理可计算出CD的长,并利用面积法可计算出OH的值;
最后连接OA,利用切线的性质得OA⊥PA,在Rt△POH中,利用勾股定理,得到![]() ,并利用垂线段最短求得PA的最小值即可.
,并利用垂线段最短求得PA的最小值即可.
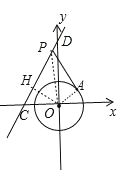
如图, 令直线y=![]() x+
x+![]() 与x轴交于点C,与y轴交于点D,作OH⊥CD于H,
与x轴交于点C,与y轴交于点D,作OH⊥CD于H,
当x=0时,y=![]() ,则D(0,
,则D(0,![]() ),
),
当y=0时,![]() x+
x+![]() =0,解得x=-2,则C(-2,0),
=0,解得x=-2,则C(-2,0),
∴![]() ,
,
∵![]() OHCD=
OHCD=![]() OCOD,
OCOD,
∴OH=![]() .
.
连接OA,如图,
∵PA为⊙O的切线,
∴OA⊥PA,
∴![]() ,
,
当OP的值最小时,PA的值最小,
而OP的最小值为OH的长,
∴PA的最小值为![]() .
.
故选D.

练习册系列答案
相关题目