题目内容
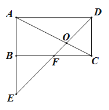
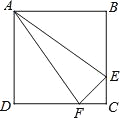
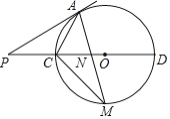
【题目】如图,过⊙O外一点P作⊙O的切线PA切⊙O于点A,连接PO并延长,与⊙O交于C、D两点,M是半圆CD的中点,连接AM交CD于点N,连接AC、CM.
(1)求证:CM2=MN.MA;
(2)若∠P=30°,PC=2,求CM的长.
【答案】(1)见解析;(2)CM=2![]() .
.
【解析】
(1)由![]() 知
知![]() ,根∠CMA=∠NMC据证ΔAMC∽ΔCMN 即可得;
,根∠CMA=∠NMC据证ΔAMC∽ΔCMN 即可得;
(2)连接OA、DM,由直角三角形PAO中∠P=30°知![]() ,据此求得OA=OC=2,再证三角形CMD是等腰直角三角形得CM的长.
,据此求得OA=OC=2,再证三角形CMD是等腰直角三角形得CM的长.
(1)![]() 中,
中,![]() 点是半圆
点是半圆![]() 的中点,
的中点,
![]()
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ;
;
(2)连接![]() 、
、![]() ,
,
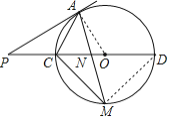
![]() 是
是![]() 的切线,
的切线,
![]() ,
,
又![]() ,
,
![]() ,
,
设![]() 的半径为
的半径为![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
又![]() 是直径,
是直径,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() 在
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,即
,即![]() ,
,
则![]() ,
,
![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目