题目内容
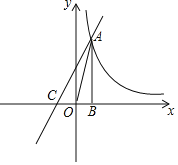
【题目】如图,已知反比例函数y=![]() 的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
(1)求m和n的值;
(2)若一次函数y=kx+2的图象经过点A,并且与x轴相交于点C,求线段AC的长.
【答案】(1)n =1,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由点A(n,4),AB⊥x轴,且点A在第一象限内,得AB=4,OB=n,利用△AOB的面积为2可求n的值,从而得到点A的坐标,代入反比例函数解析式即可求出m;
(2)代入点A坐标即可求出一次函数的解析式,从而求出与x轴交点C的坐标,利用勾股定理即可求线段AC的长.
解:(1)由点A(n,4),AB⊥x轴于点B,且点A在第一象限内,得AB=4,OB= n,
所以S△AOB=![]() ,
,
由S△AOB=2,得 n =1,
所以A(1,4),
把A(1,4)代入![]() 中,得
中,得![]() ;
;
(2)由直线![]() 过点A(1,4),得
过点A(1,4),得 ![]() ,
,
所以一次函数的解析式为![]() ;
;
令![]() ,得
,得![]()
所以点C的坐标为(-1,0),
由(1)可知OB=1, 所以BC=2,
在Rt△ABC中,![]() .
.

【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为5元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格为6元/
的价格为6元/![]() ,超过
,超过![]() 部分的价格为4元/
部分的价格为4元/![]() .设小张在同一个批发店一次购买苹果的数量为
.设小张在同一个批发店一次购买苹果的数量为![]() .
.
(1)根据题意填表:
一次购买数量/ | 20 | 50 | 150 | … |
甲批发店花费/元 | 250 | … | ||
乙批发店花费/元 | 350 | … |
(2)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若小张在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小张在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的___________批发店购买花费少;
,则他在甲、乙两个批发店中的___________批发店购买花费少;
③若小张在同一个批发店一次购买苹果花费了460元,则他在甲、乙两个批发店中的___________批发店购买数量多.