题目内容
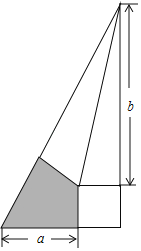
【题目】我国魏晋时期的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理．如图所示，若a＝2，b＝3，现随机向该图形内掷一枚小针，则针尖落在阴影域内的概率为_____．
【答案】
【解析】
设小正方形的边长为x，根据已知条件得到AB＝2+3＝5，根据勾股定理列方程求得x＝1，x＝﹣6（不合题意舍去），根据三角形的面积公式即可得到结论．
设小正方形的边长为x，
∵a＝2，b＝3，
∴AB＝2+3＝5，
在Rt△ABC中，AC2+BC2＝AB2，
即（2+x）2+（x+3）2＝52，
解得：x＝1，x＝﹣6（不合题意舍去），
∴S△ABC＝
×3×4＝6，S阴影＝×2×1×2＝2，
∴针尖落在阴影域内的概率＝
＝，
故答案为．
练习册系列答案
相关题目
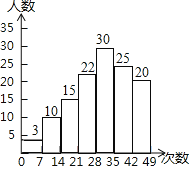
【题目】某校为了预测本校九年级男生毕业体育测试达标情况，随机抽取该年级部分男生进行了一次测试（满分50分，成绩均记为整数分），并按测试成绩
（单位：分）分成四类：
类（
），
类（
），
类（
），
类（
）绘制出如图所示的不完整条形统计图，请根据图中信息解答下列问题：
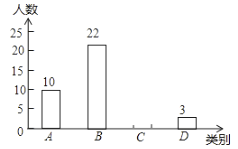
成绩等级 | 人数 | 所占百分比 |
| 10 |
|
| 22 |
|
|
|
|
| 3 |
|
（1）
______，
_______，
_________；
（2）补全条形统计图；
（3）若该校九年级男生有600名，类为测试成绩不达标，请估计该校九年级男生毕业体育测试成绩能达标的有多少名？
