题目内容
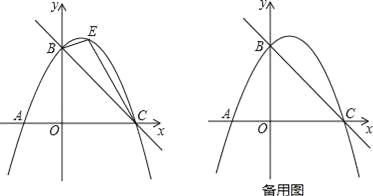
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴相交于负半轴,给出五个结论:①a+b+c=0,②abc<0,③2a+b>0,④a+c=1,⑤当﹣1<x<1时,y<0;其中正确的结论的序号( )
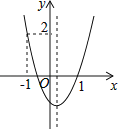
A.①③⑤B.②③④C.①③④D.②③⑤
【答案】C
【解析】
①中,抛物线点(1,0),代入可得结论;
②中,抛物线开口可判断a的符号,对称轴的位置可判断b的符号,抛物线与y轴的交点可判断c的符号;
③中,利用对称轴小于1可判断2a+b的符号;
④中,将点(﹣1,2)和(1,0)代入函数,可得a+c的值;
⑤中,根据抛物线与x轴的另一个交点在(﹣1,0)和(0,0)之间可判断y的取值范围.
解:∵抛物线经过点(1,0),即x=1时,y=0,
∴a+b+c=0,所以①正确;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴a、b异号,即b<0,
∵抛物线与y轴相交于负半轴,
∴c<0,
∴abc>0,所以②错误;
∵x=![]() <1,
<1,
而a>0,
∴﹣b<2a,
即2a+b>0,所以③正确;
∵二次函数经过点(﹣1,2)和(1,0),
∴a﹣b+c=2,a+b+c=0,
∴2a+2c=2,即a+c=1,所以④正确;
∵抛物线与x轴的另一个交点在(﹣1,0)和(0,0)之间,
∴当﹣1<x<0时,y不一定小于0,所以⑤错误.
故选:C.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】本学期,大兴区开展了“恰同学少年,品诗词美韵”中华传统诗词大赛活动![]() 小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
诗词数量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么这30名同学四月份诗词背诵数量的众数和中位数分别是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7