Question

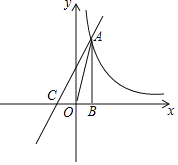
【题目】如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y＝（k≠0，x＞0）的图象同时经过顶点C，D．若点C的横坐标为5，BE＝3DE

（1）求出k值．

（2）求出△OCD的面积

（3）试探究坐标轴上是否存在点P，使得△PCD的面积等于菱形ABCD的面积的一半，如果存在，请直接写出点P的坐标；如不存在，请说明理由．

Answer 1

【答案】（1）k＝；（2）9；（3）存在，P(0，)或(1，0)

【解析】

（1）由已知，可得菱形边长为5，作DF⊥BC，设出点D坐标，即可用勾股定理构造方程，进而求出k值；

（2）连接OD、OC，构造矩形OEGH，利用矩形的面积减去三个小三角形的面积，即可得到答案；

（3）先求出菱形的面积，然后得到△PCD的面积，然后分成两种情况讨论，分别作出图形，求出点P的坐标即可.

解：（1）过点D作DF⊥BC于F，

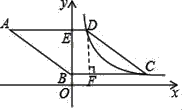
由已知，BC＝5，

∵四边形ABCD是菱形，

∴DC＝5，

∵BE＝3DE，

∴设DE＝x，则BE＝3x，

∴DF＝3x，BF＝x，FC＝5﹣x，

在Rt△DFC中，DF2+FC2＝DC2

∴（3x）2+（5﹣x）2＝52

∴解得：x＝1；

∴DE＝1，FD＝3，

设OB＝a

则点D坐标为（1，a+3），点C坐标为（5，a），

∵点D、C在双曲线上，

∴1×（a+3）＝5a，

∴a＝，

∴点C坐标为（5，），点D坐标为（1，），

∴k＝；

（2）连接OD、OC，构造矩形OEGH，如图：

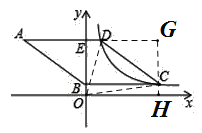
由（1）知，点C坐标为（5，），点D坐标为（1，），

∴OE=，DE=1，DG=4，CG=3，CH=，OH=5，

∴；

（3）存在；

①当点P与点B重合时，如图，连接PD；

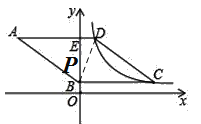
∵PD是菱形的对角线，

∴，

∴点P的坐标为：(0，)；

②如图，过点D作DP⊥x轴，交BC于点F，

由（1）可知，，

∵DP=，，

∴，

∴，

∴点P的坐标为：（1，0）；

综合上述，P的坐标为(0，)，(1，0).