ЬтФПФкШн
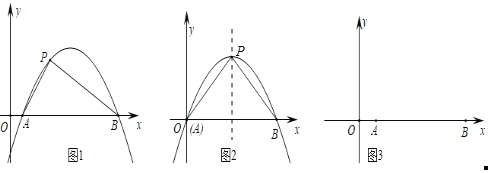
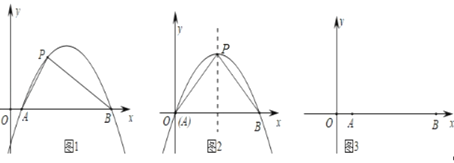
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНax2+bx+c(aЁй0)гыxжсНЛгкAЃЌBСНЕуЃЌЕуPдкХзЮяЯпЩЯ(гыAЃЌBСНЕуВЛжиКЯ)ЃЌШєЁїABPЕФШ§БпТњзуAP2+BP2ЃНAB2ЃЌдђЮвУЧГЦЕуPЮЊХзЮяЯпyЃНax2+bx+c(aЁй0)ЕФЙДЙЩЕуЃЎ
(1)жБНгаДГіХзЮяЯпyЃНx2Љ1ЕФЙДЙЩЕузјБъЮЊ_____ЃЛ
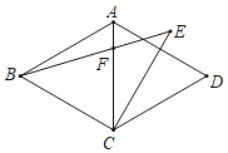
(2)ШчЭМ2ЃЌвбжЊХзЮяЯпЃКyЃНax2+bx(aЃМ0ЃЌbЃО0)гыxжсНЛгкAЁЂBСНЕуЃЌЕуPЮЊХзЮяЯпЕФЖЅЕуЃЌЮЪЕуPФмЗёЮЊХзЮяЯпЕФЙДЙЩЕуЃЌШєФмЃЌЧѓГіbЕФжЕЃЛ
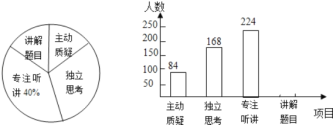
(3)ШчЭМ3ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуA(2ЃЌ0)ЃЌB(12ЃЌ0)ЃЌЕуPЕНxжсЕФОрРыЮЊ1ЃЌЕуPЪЧЙ§AЁЂBСНЕуЕФХзЮяЯпЩЯЕФЙДЙЩЕуЃЌЧѓЙ§PЁЂAЁЂBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНКЭЕуPЕФзјБъЃЎ
ЁОД№АИЁП(1)(0ЃЌЉ1)ЃЛ(2)ЕБbЃН2ЪБЃЌЕуPЮЊХзЮяЯпЕФЙДЙЩЕуЃЛ(3)ЕБЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊyЃНЉx2+14xЉ24ЪБЃЌЕуPЕФзјБъЮЊ(7Љ2![]() ЃЌ1)Лђ(7+2
ЃЌ1)Лђ(7+2![]() ЃЌ1)ЃЛЕБЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊyЃНx2Љ14x+24ЪБЃЌЕуPЕФзјБъЮЊ(7Љ2
ЃЌ1)ЃЛЕБЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊyЃНx2Љ14x+24ЪБЃЌЕуPЕФзјБъЮЊ(7Љ2![]() ЃЌЉ1)Лђ(7+2
ЃЌЉ1)Лђ(7+2![]() ЃЌЉ1)ЃЎ
ЃЌЉ1)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнХзЮяЯп![]() ПЩжЊгы
ПЩжЊгы![]() жсЕФНЛЕузјБъМА
жсЕФНЛЕузјБъМА![]() ЕФГЄЖШЃЌЩшЙДЙЩЕуЕФзјБъЮЊ
ЕФГЄЖШЃЌЩшЙДЙЩЕуЕФзјБъЮЊ![]() ЃЌдйИљОнЙДЙЩЕуЕФЖЈвхПЩЧѓГіЙДЙЩЕуЕФзјБъЃЛ
ЃЌдйИљОнЙДЙЩЕуЕФЖЈвхПЩЧѓГіЙДЙЩЕуЕФзјБъЃЛ
ЃЈ2ЃЉРћгУХфЗНЗЈПЩЧѓГіЕу![]() ЕФзјБъЃЌгЩЕу
ЕФзјБъЃЌгЩЕу![]() ЮЊХзЮяЯпЕФЙДЙЩЕуПЩжЊ
ЮЊХзЮяЯпЕФЙДЙЩЕуПЩжЊ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЧѓГі
ЮЊЕШбќжБНЧШ§НЧаЮЃЌРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЧѓГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЩшЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌгЩ
ЃЌгЩ![]() ЕН
ЕН![]() жсЕФОрРыЮЊ1ПЩжЊ
жсЕФОрРыЮЊ1ПЩжЊ![]() ЃЌИљОнЙДЙЩЕуЕФЖЈвхПЩСаГіЙигк
ЃЌИљОнЙДЙЩЕуЕФЖЈвхПЩСаГіЙигк![]() ЕФвЛдЊЖўДЮЗНГЬЃЌМДПЩЕУГіЕу
ЕФвЛдЊЖўДЮЗНГЬЃЌМДПЩЕУГіЕу![]() ЕФзјБъЃЌгЩЕу
ЕФзјБъЃЌгЩЕу![]() Ш§ЕуПЩЩшХзЮяЯпЕФНтЮіЪНЮЊ
Ш§ЕуПЩЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌгЩ
ЃЌгЩ![]() ЕФзјБъРћгУЯЕЪ§Д§ЖЈЗЈПЩЧѓГіИУХзЮяЯпЕФНтЮіЪН.
ЕФзјБъРћгУЯЕЪ§Д§ЖЈЗЈПЩЧѓГіИУХзЮяЯпЕФНтЮіЪН.
НтЃК(1)ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
НтжЎЕУЃК![]() ЃЌ
ЃЌ
ЁрЕуAЕФзјБъЮЊ![]() ЃЌЕуBЕФзјБъЮЊ
ЃЌЕуBЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЩшХзЮяЯп![]() ЕФЙДЙЩЕузјБъЮЊ
ЕФЙДЙЩЕузјБъЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
ЁрХзЮяЯп![]() ЕФЙДЙЩЕузјБъЮЊ
ЕФЙДЙЩЕузјБъЮЊ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ
(2)Ёп![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ШєЕуPФмЮЊХзЮяЯпЕФЙДЙЩЕуЃЌдђ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЮЊЕШбќжБНЧШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁрЕБ![]() ЪБЃЌЕуPЮЊХзЮяЯпЕФЙДЙЩЕуЃЎ
ЪБЃЌЕуPЮЊХзЮяЯпЕФЙДЙЩЕуЃЎ
(3)ЩшЕуPЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁпЕуPЕНxжсЕФОрРыЮЊ1ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌЕуAЕФзјБъЮЊ
ЃЌЕуAЕФзјБъЮЊ![]() ЃЌЕуBЕФзјБъЮЊ
ЃЌЕуBЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ИљОнСНЕужЎМфЕФОрРыЙЋЪН
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
ЁрЕуPЕФзјБъЮЊ![]() ЃЌЃЎ
ЃЌЃЎ
ЩшЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЕБЕуPЕФзјБъЮЊ![]() ЪБЃЌНЋ
ЪБЃЌНЋ![]() ДњШы
ДњШы![]() ЃЌНтжЎЕУЃК
ЃЌНтжЎЕУЃК
![]() ЃЌ
ЃЌ
ЁрЩшЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
ЭЌРэЃКЕБЕуPЕФзјБъЮЊ![]() ЪБЃЌЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ
ЪБЃЌЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЕБЕуPЕФзјБъЮЊ![]() ЪБЃЌЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ
ЪБЃЌЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЕБЕуPЕФзјБъЮЊ![]() ЪБЃЌЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ
ЪБЃЌЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКЕБЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ![]() ЪБЃЌЕуPЕФзјБъЮЊ
ЪБЃЌЕуPЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЕБЙ§PЃЌAЃЌBШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊ![]() ЪБЃЌЕуPЕФзјБъЮЊ
ЪБЃЌЕуPЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ