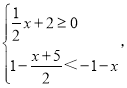题目内容
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
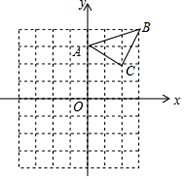
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
【答案】(1)(2,-2);(2)(1,0);(3)10.
【解析】试题分析:(1)将点A、B、C分别向左平移4个单位得到对应点,再顺次连接可得;
(2)利用位似图形的性质得出对应点位置,进而得出答案;
(3)割补法求解可得.
试题解析:
(1)如图,△A1B1C1即为所求,点C1的坐标是(﹣2,2),
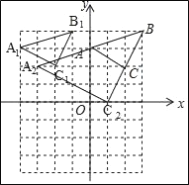
故答案为:(﹣2,2);
(2)如图所示,△A2B2C2即为所求,点C2的坐标是(1,0),
故答案为:(1,0);
(3)△A2B2C2的面积![]() ×(2+4)×6﹣
×(2+4)×6﹣![]() ×2×4﹣
×2×4﹣![]() ×2×4=10,
×2×4=10,
故答案为:10

练习册系列答案
相关题目
【题目】为选拔参加八年级数学“拓展性课程”活动人选,数学李老师对本班甲、乙两名学生以前经历的10次测验成绩(分)进行了整理、分析(见图①):
学生 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 83.7 | a | 86 | 13.21 |
乙 | 83.7 | 82 | b | 46.21 |
(1)写出a,b的值;
(2)如要推选1名学生参加,你推荐谁?请说明你推荐的理由.