Question

【题目】如图，在菱形ABCD中，∠BAD＝120°，CE⊥AD，且CE＝BC，连接BE交对角线AC于点F，则∠EFC＝_____°．

Answer 1

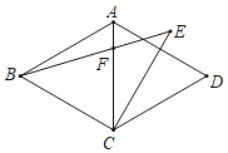
【答案】105°

【解析】

由菱形及菱形一个内角为120°，可得△ABC与△ACD为等边三角形．CE⊥AD可由三线合一得CE平分∠ACD，即求得∠ACE的度数．再由CE=BC可求出∠E的度数，根据三角形内角和即可得∠EFC的度数．

解：∵菱形ABCD中，∠BAD＝120°

∴AB＝BC＝CD＝AD，∠BCD＝120°，∠ACB＝∠ACD＝ ∠BCD＝60°，

∴△ACD是等边三角形

∵CE⊥AD

∴∠ACE＝∠ACD＝30°

∴∠BCE＝∠ACB+∠ACE＝90°

∵CE＝BC

∴∠E＝∠CBE＝45°

∴∠EFC＝180°﹣∠E﹣∠ACE＝180°﹣45°﹣30°＝105°

故答案为：105°