题目内容
【题目】如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面
的最大距离是5m．
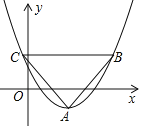
（1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如下图）
你选择的方案是_____（填方案一，方案二，或方案三），则B点坐标是______，求出你所选方案中的抛物线的表达式；
（2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．
【答案】（1）方案1，点B的坐标为（5，0），
；方案2，点B的坐标为（10，0），
；方案3，点B的坐标为（5， 
），
；（2）3.2．
【解析】试题分析：（1）根据抛物线在坐标系的位置，可用待定系数法求抛物线的解析式．
（2）把x=3代入抛物线的解析式，即可得到结论．
试题解析：解：方案1：（1）点B的坐标为（5，0），设抛物线的解析式为： 
．由题意可以得到抛物线的顶点为（0，5），代入解析式可得： 
，∴抛物线的解析式为： 
；
（2）由题意：把
代入
，解得： 
=3.2，∴水面上涨的高度为3.2m．
方案2：（1）点B的坐标为（10，0）．设抛物线的解析式为： 
．
由题意可以得到抛物线的顶点为（5，5），代入解析式可得： 
，∴抛物线的解析式为： 
；
（2）由题意：把
代入
解得： 
=3.2，∴水面上涨的高度为3.2m．
方案3：（1）点B的坐标为（5， 
），由题意可以得到抛物线的顶点为（0，0）．
设抛物线的解析式为： 
，把点B的坐标（5， 
），代入解析式可得： 
，
∴抛物线的解析式为： 
；
（2）由题意：把
代入
解得： 
=
，∴水面上涨的高度为
3.2m．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
