题目内容
【题目】如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,
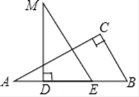
(1)试说明△ABC与△MED全等;
(2)若∠M=35°,求∠B的度数?
【答案】(1)见解析;(2)55°.
【解析】
(1)根据平行线的性质可得出∠B=∠MED,结合全等三角形的判定定理可判断△ABC≌△MED.
(2)在△MDE中,∠MDE=90°,∠M=35°,故∠MED可求,又∠B=∠MED,即可得出答案.
解:(1)证明:∵MD⊥AB,
∴∠MDE=∠C=90°,
∵ME∥BC,
∴∠B=∠MED,
在△ABC与△MED中,
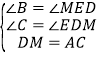 ,
,
∴△ABC≌△MED(AAS).
(2)∵在△MDE中,∠MDE=90°,∠M=35°,
∴∠MED =180°-90°-35°=55°,
又∵△ABC≌△MED,
∴∠B=∠MED=55°.
所以∠B的度数为55°.

练习册系列答案
相关题目